
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 到
到![]() 三个顶点的距离相等;⑤
三个顶点的距离相等;⑤![]() .其中正确的结论有( )个.
.其中正确的结论有( )个.
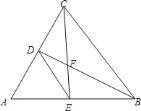
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
利用三角形的内角和,角平分线的性质可得∠CFD=120°,所以∠BFE=60°,并且有条件易知F为三角形的内心,若想证明BE+CD=BC,只能给BE,CD找相等的线段代替,自然想到构造全等三角形.
(1)∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD,∠ACE=∠BCE,
∴∠CBD+∠BCE=60°,
∴∠BFE=60°,
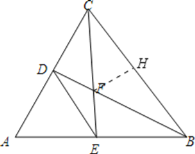
∴②cos∠BFE=![]() ,正确.
,正确.
(2)∵∠ABC,∠ACB的平分线分别交AC、AB于点D,E,CE、BD相交于点F,
∴F为三角形的内心,
∴④点F到△ABC三边的距离相等错误.
(3)在BC上截取BH=BE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴△EBF≌△HBF,
∴∠EFB=∠HFB=60°.
由(1)知∠CFB=120°,
∴∠CFH=60°,
∴∠CFH=∠CFD=60°,
又∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴△CDF≌△CHF.
∴CD=CH,
∵CH+BH=BC,
∴⑤BE+CD=BC正确.
∵△CDF≌△CFH,
∴DF=FH,
∵△FEB≌△HFB,
∴FE=FH
∵DF=FH,FE=FH,
∴DF=FE,△DEF为等腰三角形,
∴∠EDF=∠FED
故③正确.
题目现有的条件不能够证明①,所以①④错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,河流两岸![]() 、
、![]() 平行,
平行,![]() 、
、![]() 是河岸
是河岸![]() 上间隔
上间隔![]() 米的两根电线杆,某人在河岸
米的两根电线杆,某人在河岸![]() 上的
上的![]() 处测得
处测得![]() ,然后沿河岸走了
,然后沿河岸走了![]() 米到达
米到达![]() 处,测得
处,测得![]() ,则河流的宽度
,则河流的宽度![]() 的值为________
的值为________![]() (结果精确到个位,
(结果精确到个位,![]() ,
,![]() )
)
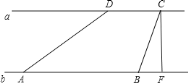
查看答案和解析>>
科目:初中数学 来源: 题型:
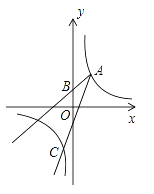
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
科目:初中数学 来源: 题型:
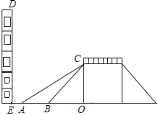
【题目】如图是某一过街天桥的示意图,天桥高![]() 为
为![]() 米,坡道倾斜角
米,坡道倾斜角![]() 为
为![]() ,在距
,在距![]() 点
点![]() 米处有一建筑物
米处有一建筑物![]() .为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角
.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角![]() 处之间地面要留出不少于
处之间地面要留出不少于![]() 米宽的人行道.
米宽的人行道.
![]() 若将倾斜角改建为
若将倾斜角改建为![]() (即
(即![]() ),则建筑物
),则建筑物![]() 是否要拆除?(
是否要拆除?(![]() )
)
![]() 若不拆除建筑物
若不拆除建筑物![]() ,则倾斜角最小能改到多少度(精确到
,则倾斜角最小能改到多少度(精确到![]() )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
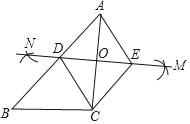
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )
A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,射线
,射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设点
的速度运动,设点![]() 运动的时间为
运动的时间为![]() .
.
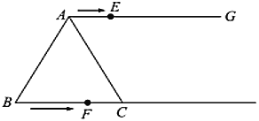
(1)当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() _________
_________![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上运动时,
的延长线上运动时,![]() _________
_________![]() (请用含
(请用含![]() 的式子表示);
的式子表示);
(2)在整个运动过程中,当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() 的值;
的值;
(3)求当![]() _________时,
_________时,![]() ,
,![]() 两点间的距离最小.
两点间的距离最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com