
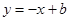 (b>0)与双曲线
(b>0)与双曲线 (
(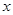 >0)交于A、B两点,连接OA、OB, AM⊥
>0)交于A、B两点,连接OA、OB, AM⊥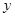 轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB=
轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB= 时,ON=BN=1,其中结论正确的是( )
时,ON=BN=1,其中结论正确的是( )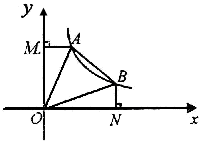
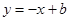 与
与 ,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;
,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论; 时,GA=GB=1,则ON-BN=GN-BN=GB=1.
时,GA=GB=1,则ON-BN=GN-BN=GB=1. 中,得x1•y1=x2•y2=k,
中,得x1•y1=x2•y2=k,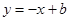 与
与 ,得x2-bx+k=0,
,得x2-bx+k=0,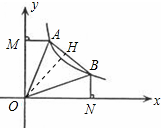
 k+
k+ k=k,正确;
k=k,正确;
 时,GA=GB=1,
时,GA=GB=1,

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源:不详 题型:单选题
 是
是 轴正半轴上的一个定点,点
轴正半轴上的一个定点,点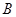 是双曲线
是双曲线 (
( )上的一个动点,当点
)上的一个动点,当点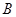 的横坐标逐渐增大时,
的横坐标逐渐增大时,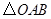 的面积将会( )
的面积将会( )
| A.逐渐增大 | B.不变 | C.逐渐减小 | D.先增大后减小 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com