

���� ��1���������εı߳�Ϊa�����PB���ɽ�����⣮
��2������֤����ADE�ա�CDE���Ƴ���AED=��DEC=��AEC=120�㣬AE=EC����DCE=��DAE=15�㣬��PCE=75�㣬�ɡ�APB=60�㣬�Ƴ���APB+��AEC=120�㣬�Ƴ�A��P��C��E�ĵ㹲Բ������AE=��EC���Ƴ���APE=��EPC=30�㣬�Ƴ���PEC=75��=��PCE���Ƴ�PE=PC����PB=a��PA=2a��AB=BC=$\sqrt{3}$a��
��PA+PC=2a+a+$\sqrt{3}$a=$\sqrt{3}$��$\sqrt{3}$a+a��=$\sqrt{3}$��BC+PB��=$\sqrt{3}$PC����֤����
��3����ͼ3�У����ۣ�$\frac{DF}{AB}$=$\frac{\sqrt{6}}{2}$������BD��AC��O����FM��AC��M��DF��AC���ڵ�H����AC=BD=4a����OA=OC=OD=OB=2a��AD=2$\sqrt{2}$a����취���DF���ɽ�����⣮
��� ��1���⣺��ͼ1�У��������εı߳�Ϊa��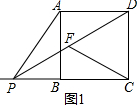
���ı���ABCD�������Σ�
���ABC=��DCB=��ABP=90�㣬
�ߡ�CDF�ǵȱ������Σ�
���FDC=��FCD=60�㣬
���FPC=��FCP=30�㣬
��PF=DF=CF=CD=a��
��PC=$\sqrt{P{D}^{2}-C{D}^{2}}$=$\sqrt{3}$a��
��PB=$\sqrt{3}$a-a��
��tan��PAB=$\frac{PB}{AB}$=$\frac{PB}{AB}$=$\frac{\sqrt{3}a-a}{a}$=$\sqrt{3}$-1��
��2��֤������ͼ2�У�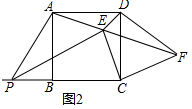
�ߡ�CDF�ǵȱ������Σ��ı���ABCD�������Σ�
��CD=DF=AD�����ADC=90�㣬��CDF=60�㣬
���ADF=150�㣬��DAF=��DFA=15�㣬
�ߡ�EDA=��EDC=45�㣬
���AED=180��-��DAE-��ADE=120�㣬
�ڡ�ADE�͡�CDE�У�
$\left\{\begin{array}{l}{DA=DC}\\{��ADE=��CDE}\\{DE=DE}\end{array}\right.$��
���ADE�ա�CDE��
���AED=��DEC=��AEC=120�㣬AE=EC����DCE=��DAE=15�㣬
���PCE=75�㣬
�ߡ�APB=60�㣬
���APB+��AEC=120�㣬
��A��P��C��E�ĵ㹲Բ��
����AE=��EC��
���APE=��EPC=30�㣬
���PEC=75��=��PCE��
��PE=PC����PB=a��PA=2a��AB=BC=$\sqrt{3}$a��
��PA+PC=2a+a+$\sqrt{3}$a=$\sqrt{3}$��$\sqrt{3}$a+a��=$\sqrt{3}$��BC+PB��=$\sqrt{3}$PC��
��PA+PC=$\sqrt{3}$PE��
��3���⣺��ͼ3�У����ۣ�$\frac{DF}{AB}$=$\frac{\sqrt{6}}{2}$��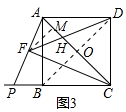
���ɣ�����BD��AC��O����FM��AC��M��DF��AC���ڵ�H����AC=BD=4a����OA=OC=OD=OB=2a��AD=2$\sqrt{2}$a��
��S��AFC��S������ABCD=1��4��
��$\frac{1}{2}$•AC•FM��AD2=1��4��
��$\frac{1}{2}$•4a•FM��8a2=1��4��
��FM=a��
��AF��FC��FM��AC����֪��AFM�ס�FCM��
��FM2=AM•MC��
��AM•��4a-AM��=a2��
��AM2-4a•AM+a2=0��
��AM=��2-$\sqrt{3}$��a��2+$\sqrt{3}$��a����������
��FM��OD��
��$\frac{HM}{HO}$=$\frac{FH}{DH}$=$\frac{FM}{OD}$=$\frac{1}{2}$��
��HM=$\frac{1}{3}$$\sqrt{3}$a��OH=$\frac{2}{3}$$\sqrt{3}$a��
��FH=$\sqrt{F{M}^{2}+H{M}^{2}}$=$\frac{2\sqrt{3}}{3}$a��
��DH=2FH=$\frac{4\sqrt{3}}{3}$a��
��DF=FH+DH=2$\sqrt{3}$a��
��$\frac{DF}{AB}$=$\frac{2\sqrt{3}a}{2\sqrt{2}a}$=$\frac{\sqrt{6}}{2}$��
���� ���⿼���ı����ۺ��⣮�����ε����ʡ��ȱ������ε����ʡ�ȫ�������ε��ж������ʣ�ƽ���ߵȷ��߶ζ��������ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò���������⣬�������������ν�ϵ�˼�룬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �Ϻ��г���շѱ� | ||
| ������ | �ռ�� ��5��00��23��00�� | ҹ��� ��23��00������5��00�� |
| 0��3���� | 14Ԫ | 18Ԫ |
| 3��10���� | 2.4Ԫ/�������3���ﲿ�֣� | 3.1Ԫ/�������3���ﲿ�֣� |
| 10�������� | 3.6Ԫ/�������10���ﲿ�֣� | 4.7Ԫ/�������10���ﲿ�֣� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У���F��AD�ϣ�$\frac{DF}{FA}$=$\frac{1}{2}$��BF��AC���ڵ�P��BF��CD���ӳ��߽��ڵ�G������DP���ӳ���AB�ڵ�E��
��ͼ����?ABCD�У���F��AD�ϣ�$\frac{DF}{FA}$=$\frac{1}{2}$��BF��AC���ڵ�P��BF��CD���ӳ��߽��ڵ�G������DP���ӳ���AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
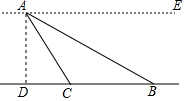 ��ͼ��һ�Ѿȴ��ں���A������Ǻ�ʧ�¿ͻ��ĵ�һ����ϻ�ӵĸ��ǡ�EACΪ60�㣬�ڶ�����ϻ�ӵĸ��ǡ�EABΪ30�㣬�˴��������ADΪ3ǧ�ף���������ϻ�ӵľ���BC�ij�����ȡ$\sqrt{3}$��1.73����ȷ��0.1ǧ�ף�
��ͼ��һ�Ѿȴ��ں���A������Ǻ�ʧ�¿ͻ��ĵ�һ����ϻ�ӵĸ��ǡ�EACΪ60�㣬�ڶ�����ϻ�ӵĸ��ǡ�EABΪ30�㣬�˴��������ADΪ3ǧ�ף���������ϻ�ӵľ���BC�ij�����ȡ$\sqrt{3}$��1.73����ȷ��0.1ǧ�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ı���ABCD�ڽ��ڡ�O����P��CD���ӳ����ϣ���AP��BD����֤��PD•BC=AB•AD��
�ı���ABCD�ڽ��ڡ�O����P��CD���ӳ����ϣ���AP��BD����֤��PD•BC=AB•AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
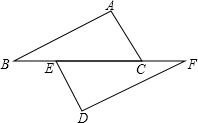 ��ͼ��ʾ����B��F��C��E��ͬһ��ֱ���ϣ�AB��DF��AC��DE��BE=CF��AB��DF�������˵�����ɣ�
��ͼ��ʾ����B��F��C��E��ͬһ��ֱ���ϣ�AB��DF��AC��DE��BE=CF��AB��DF�������˵�����ɣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com