解:(1)∵BE平分∠ABC,∠ACB=90°,EF⊥AB,垂足为F,
∴EF=CE.
在△BFE与△BCE中,∠C=∠BFE=90°,

,
∴△BFE≌△BCE,
∴BF=BC=8.
∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=10,
∴AF=AB-BF=2.
设EF=x,则CE=x,AE=6-x,
在直角△AEF中,由勾股定理,得AE
2=EF
2+AF
2,
∴(6-x)
2=x
2+2
2,
解得x=
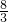
;
(2)∵在△BCE中,∠CEB=90°-∠CBE,
∠CGE=∠DGB=90°-∠DBG,
∠CBE=∠DBG,
∴∠CEB=∠CGE,
∴CE=CG;

(3)∵CD⊥AB,EF⊥AB,∴CD∥EF,
∵EF=CE,CE=CG,∴EF=CG,
∴四边形CEFG是平行四边形,
又∵CE=CG,
∴?CEFG是菱形.
分析:(1)先根据角平分线的性质,得出EF=CE,然后在直角△AEF中,运用勾股定理即可求出EF的长度;
(2)在△CEG中证明∠CEG=∠CGE即可得出结论;
(3)先根据有一组对边平行且相等的四边形是平行四边形得出四边形CEFG是平行四边形,再根据菱形的定义证明出四边形CEFG是菱形.
点评:本题考查了角平分线的性质定理,勾股定理,等腰三角形的判定及菱形的判定,综合性较强,难度中等.

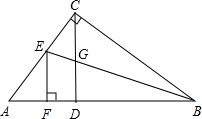
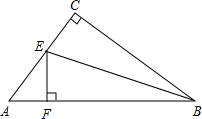 如图,已知在Rt△ABC中,∠ACB=90°,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F.
如图,已知在Rt△ABC中,∠ACB=90°,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F. ,
,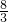 ;
; (2)∵在△BCE中,∠CEB=90°-∠CBE,
(2)∵在△BCE中,∠CEB=90°-∠CBE, (3)∵CD⊥AB,EF⊥AB,∴CD∥EF,
(3)∵CD⊥AB,EF⊥AB,∴CD∥EF,
