

分析 (1)根据直线解析式求出点M、N的坐标,再根据图2判断出CM的长,然后求出OC,从而得到点C的坐标,根据被截线段在一段时间内长度不变可以判断出先经过点B后经过点D;
(2)根据图2求出BM=10,再求出OB,然后写出点B的坐标,利用勾股定理列式求出CD,再求出BC的长度,从而得到BC=CD,判断出?ABCD是菱形,再求出MN⊥CD,根据菱形的性质可知n=DO,根据向左平移横坐标减表示出平移后的直线解析式,把点D的坐标代入函数解析式求出t的值即为a;
(3)分三种情况分段讨论即可.
解答 解:(1)令y=0,则$\frac{3}{4}$ x-6=0,解得x=8,
令x=0,则y=-6,
∴点M(8,0),N(0,-6)
∴OM=8,ON=6,
由图2可知5秒后直线经过点C,
∴CM=5,OC=OM-CM=8-5=3,
∴C(3,0),
∵10秒~a秒被截线段长度不变,
∴先经过点B;
故填:(3,0);B
(2)由图2可知BM=10,
∴OB=BM-OM=10-8=2,
∴B(-2,0),
在Rt△OCD中,由勾股定理得,CD=$\sqrt{O{D}^{2}+O{C}^{2}}=\sqrt{{4}^{2}+{3}^{2}}$=5,
∴BC=CD=5,
∴?ABCD是菱形,
∵$\frac{OC}{OD}=\frac{ON}{OM}=\frac{3}{4}$,
∴MN⊥CD,
∴n=DO=4
∵设直线MN向x轴负方向平移的速度为每秒1个单位的长度,
平移后的直线解析式为y=$\frac{3}{4}$ (x+t)-6,
把点D(0,4)代入得,$\frac{3}{4}$(0+t)-6=4,
解得t=$\frac{40}{3}$,
∴a=$\frac{40}{3}$;
故答案为:(1)(3,0),B;(2)(-2,0),4,$\frac{40}{3}$;
(3)当0≤t≤5时,y=0;
当5<t≤10,如图1,该直线与BC、CD分别交于F、E,FC=t-5,
∵直线CD的解析式为:y=-$\frac{4}{3}$x+4,
∴EF⊥CD,
∴△CEF∽△COD,
∴$\frac{CF}{CD}=\frac{EF}{OD}=\frac{CE}{OC}$,
∴$\frac{t-5}{5}=\frac{EF}{4}=\frac{CE}{3}$,
∴EF=$\frac{4(t-5)}{5}$,CE=$\frac{3(t-5)}{5}$,
∴y=$\frac{1}{2}$×$\frac{4(t-5)}{5}$×$\frac{3(t-5)}{5}$=$\frac{6(t-5)^{2}}{25}$=$\frac{6}{25}$t2-$\frac{12}{5}$t+6,
当10<t≤$\frac{40}{3}$,如图2,直线与AB、CD分别交于G、E,与射线CB交于F,FB=t-10,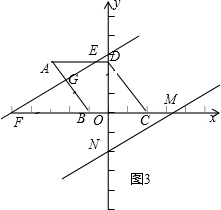
∵△BGF∽△COD,
∴$\frac{BF}{CD}=\frac{GF}{OD}=\frac{BG}{OC}$
∴FG=$\frac{4(t-10)}{5}$,BG=$\frac{3(t-10)}{5}$,
y=S△CEF-S△BGF=$\frac{6(t-5)^{2}}{25}$-$\frac{6(t-10)^{2}}{25}$=$\frac{6}{25}$(10t-75)=$\frac{12}{5}$t-18,
当$\frac{40}{3}<t<\frac{55}{3}$时,如图3,BG=$\frac{3(t-10)}{5}$,AG=5-$\frac{3(t-10)}{5}$,
∵△EAG∽△DCO,
∵$\frac{AG}{OC}$=$\frac{EG}{OD}$,
∴DG=$\frac{4}{3}$×(5-$\frac{3(t-10)}{5}$),
∴y=20-$\frac{1}{2}×$(5-$\frac{3(t-10)}{5}$)×$\frac{4}{3}$×(5-$\frac{3(t-10)}{5}$)=$\frac{6}{25}\\;{t}^{2}$t2-$\frac{44}{5}$t-$\frac{182}{3}$,
当t≥$\frac{55}{3}$时y=20.
综上所述:
y=$\left\{\begin{array}{l}{0}&{(0≤t≤5)}\\{\frac{6}{25}{t}^{2}-\frac{12}{5}t+6}&{(5<t≤10)}\\{\frac{12}{5}t-18}&{(10<t≤\frac{40}{3})}\\{\frac{6}{25}{t}^{2}-\frac{44}{5}t-\frac{182}{3}}&{(\frac{40}{3}<t<\frac{55}{3})}\\{20}&{(t≥\frac{55}{3})}\end{array}\right.$.
点评 本题是一次函数综合题型,主要利用了平行四边形的性质,菱形的判定与性质,一次函数图象的平移,待定系数法求一次函数解析式,表示出平移后的直线MN的解析式是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2m}$+$\sqrt{3m}$=$\sqrt{5m}$ | B. | 5$\sqrt{5}$-$\sqrt{5}$=4 | C. | 5+$\sqrt{2}$=5$\sqrt{2}$ | D. | m$\sqrt{x}$-n$\sqrt{x}$=(m-n)$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3-x}$ | B. | $\sqrt{x+3}$ | C. | $\sqrt{x-3}$ | D. | $\sqrt{\frac{1}{x-3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
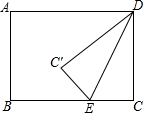 如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com