
【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)在坐标轴上找一点![]() ,使以
,使以![]() 为腰的
为腰的![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)m=4,l2的解析式为![]() ;(2)5;(3)点P的坐标为(
;(2)5;(3)点P的坐标为(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).
【解析】
(1)先求得点C的坐标,再运用待定系数法即可得到l2的解析式;
(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,再根据A(10,0),B(0,5),可得AO=10,BO=5,进而得出S△AOC-S△BOC的值;
(3)由等腰三角形的定义,可对点P进行分类讨论,分别求出点P的坐标即可.
解:(1)把C(m,3)代入一次函数![]() ,可得
,可得
![]() ,
,
解得m=4,
∴C(4,3),
设l2的解析式为y=ax,则3=4a,
解得:a=![]() ,
,
∴l2的解析式为:![]() ;
;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,

由![]() ,令x=0,则y=5;令y=0,则x=10,
,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC-S△BOC=![]() ×10×3
×10×3![]() ×5×4=15-10=5;
×5×4=15-10=5;
(3)∵![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
则点P的位置有6种情况,如图:

∵点C的坐标为:(4,3),
∴![]() ,
,
∴![]() ,
,
∴点P的坐标为:(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点Q,使得以A、C、Q为顶点的三角形为直角三角形?若存在,试求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a、b,那么![]() 的值为( ).
的值为( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧;
是以点O为圆心,OA1为半径的圆弧;![]() 是以点C为圆心,CA2为半径的圆弧;
是以点C为圆心,CA2为半径的圆弧;![]() 是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________
是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,折叠纸片,使点
,折叠纸片,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,且
,且![]() .
.
①求证:![]() ;
;
②点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位的速度运动到点
以每秒1个单位的速度运动到点![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止,点
后停止,点![]() 在整个运动过程中用时最少多少秒?
在整个运动过程中用时最少多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | -2 | - | m | 2 | 1 | 2 | 1 | - | -2 | … |
其中m=____________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)根据函数图象
①写出该函数的一条性质_______________;
②直线![]() 经过点(-l,2),若关于x的方程
经过点(-l,2),若关于x的方程![]() 有4个互不相等的实数根,则b的取值范围是__________________.
有4个互不相等的实数根,则b的取值范围是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行班际电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表:

通过计算可知两组数据的方差分别为S2甲=2.0,S2乙=2.7,则下列说法:①两组数据的平均数相同;②甲组学生比乙组学生的成绩稳定;③两组学生成绩的中位数相同;④两组学生成绩的众数相同.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 向下平移4个单位得到直线
向下平移4个单位得到直线![]() ,已知直线
,已知直线![]() 刚好过点
刚好过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,下列结论:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0.其中正确的个数是( )
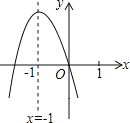
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com