
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
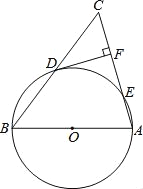
(1)求证:DF为⊙O的切线;
(2)若cosC=![]() ,CF=9,求AE的长.
,CF=9,求AE的长.
【答案】(1)证明见解析;(2)7.
【解析】
试题分析:(1)连接OD,AD,求出OD∥AC,推出OD⊥DF,根据切线的判定推出即可;
(2)求出CD、DF,推出四边形DMEF和四边形OMEN是矩形,推出OM=EN,EM=DF=12,求出OM,即可求出答案.
试题解析:(1)连接OD,AD,
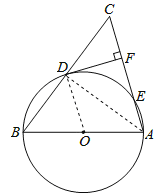
∵AB是⊙的直径,
∴∠ADB=90°,
又∵AB=AC,
∴BD=CD
又∵OB=OA,
∴OD∥AC
∵DF⊥AC,
∴OD⊥DF
又∵OD为⊙的半径,
∴DF为⊙O的切线.
(2)连接BE交OD于M,过O作ON⊥AE于N,
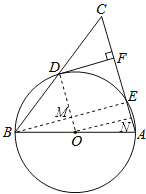
则AE=2NE,
∵cosC=![]() ,CF=9,
,CF=9,
∴DC=15,
∴DF=![]() =12,
=12,
∵AB是直径,
∴∠AEB=∠CEB=90°,
∵DF⊥AC,OD⊥DF,
∴∠DFE=∠FEM=∠MDF=90°,
∴四边形DMEF是矩形,
∴EM=DF=12,∠DME=90°,DM=EF,
即OD⊥BE,
同理四边形OMEN是矩形,
∴OM=EN,
∵OD为半径,
∴BE=2EM=24,
∵∠BEA=∠DFC=90°,∠C=∠C,
∴△CFD∽△CEB,
∴![]() ,
,
∴![]() ,
,
∴EF=9=DM,
设⊙O的半径为R,
则在Rt△EMO中,由勾股定理得:R2=122+(R-9)2,
解得:R=![]() ,
,
则EN=OM=![]() -9=
-9=![]() =
=![]() ,
,
∴AE=2EN=7.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD为BC边上的的中线,则S△ABD= S△ADC.

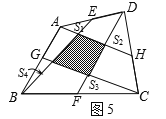
实践探究
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为 ;
(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为 ;
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为 ;
解决问题:
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和是多少?即求S1+ S2+ S3+ S4=?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家游泳中心——“水立方”是北京2008年奥运会场馆之一,它的外层膜的展开面积约为260000平方米,将260000用科学记数法表示应为( )
A. 2.6×105 B. 26×104 C. 0.26×102 D. 2.6×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,关于x 的一元二次方程是( )
A. x—2x—3=0 B. x- 2y- 1=0
C. x-x(x+3)=0 D. ax+bx +c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
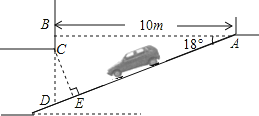
【题目】为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() .按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算
.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算![]() 的长,并标明限制高度.(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
的长,并标明限制高度.(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)(精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ.给出如下结论:
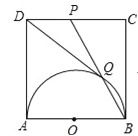
①DQ与半圆O相切;②![]() ;③∠ADQ=2∠CBP;④cos∠CDQ=
;③∠ADQ=2∠CBP;④cos∠CDQ=![]() .其中正确的是 (请将正确结论的序号填在横线上).
.其中正确的是 (请将正确结论的序号填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com