【答案】
分析:(1)通过解方程,首先求出A、B两点的坐标,再利用待定系数法求出抛物线的解析式.
(2)①由于没有明确等腰△BDE的腰和底,所以要分类进行讨论:
Ⅰ、BD为底,此时点P在线段BD的中垂线上,B、D的坐标已知,则E点横坐标可求,在求出直线BC的解析式后代入其中即可确定点E的坐标;
Ⅱ、DE为底,那么BE=BD=2,在Rt△BOC中,∠DBE的正弦、余弦值不难得出,所以过E作x轴的垂线,在构建的直角三角形中,通过解直角三角形来确定点E的坐标;
Ⅲ、BE为底,解法与Ⅱ类似,唯一不同的是需要过D作BE的垂线,通过构建直角三角形首先求出BE的长.
②△CDP中,线段CD的位置是确定的,所以以CD为底进行讨论,欲使△CDP的面积最大,必须令点P到直线CD的距离最长,若做一条与直线CD平行的直线,当该直线与抛物线有且只有一个交点时,这个唯一的交点就是符合条件的P点,理清大致思路后,具体的解法便不难得出:首先求出直线CD的解析式,然后过P作直线l∥直线CD,且点P为直线l与抛物线的唯一交点,由于直线l、CD平行,所以它们的斜率相同,联立抛物线的解析式后即可求出交点P的坐标,然后过P作x轴的垂线,通过图形间的面积和差关系求出△CDP的面积最大值.
解答:解:(1)解方程x
2-3x-4=0,得:x
1=-1、x
2=4,则 A(-1,0)、B(4,0);
依题意,设抛物线的解析式:y=a(x+1)(x-4),代入C(0,-2),得:
a(0+1)(0-4)=-2,
解得:a=

故抛物线的解析式:y=

(x+1)(x-4)=

x
2-

x-2.
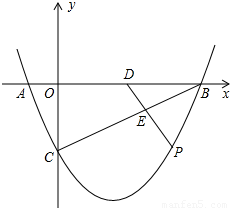
(2)①分三种情况讨论:
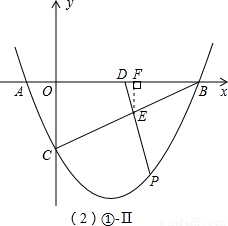
Ⅰ、当DE=BE时(如图①-Ⅰ),点E在线段BD的中垂线上,则E点横坐标为3;
由C(0,-2)、B(4,0)得,直线BC:y=

x-2;
当x=3时,y=

x-2=-

,即 E(3,-

);
Ⅱ、当BE=BD时(如图①-Ⅱ),BE=BD=2;
在Rt△OBC中,sin∠DBE=
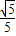
,cos∠DBE=
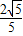
;
过E作EF⊥x轴于点F,则有:
在Rt△BEF中,EF=BE•sin∠DBE=2•
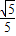
=
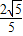
,BF=BE•cos∠DBE=
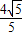
,
则OF=OB-BF=4-
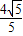
,即 E(4-
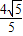
,-
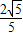
);
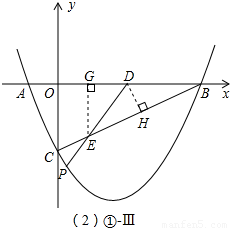
Ⅲ、当BD=DE时(如图①-Ⅲ),DE=BD=2;
过D作DH⊥BC于H,过E作EG⊥x轴于G,则有:
在Rt△BDH中,同Ⅱ可求得BH=
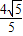
,则 BE=2BH=
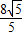
;
在Rt△BEG中,EG=BE•sin∠DBE=
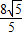
•
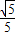
=

,BG=BE•cos∠DBE=
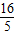
,
则OG=OB-BG=

,即 E(

,-

);
综上,当BE=DE时,E(3,-

);当BE=BD时,E(4-
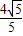
,-
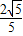
);当BD=DE时,E(

,-

).
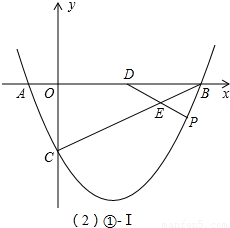
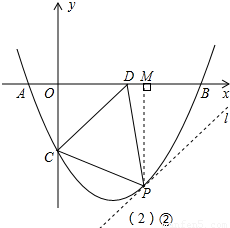
②由C(0,-2)、D(2,0)得,直线CD:y=x-2;
作直线l∥CD,且直线l与抛物线有且只有一个交点P,设直线l:y=x+b,联立抛物线的解析式:
x+b=

x
2-

x-2,即:

x
2-

x-2-b=0
△=
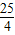
-4×

×(-2-b)=0,解得 b=-
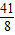
即,直线l:y=x-
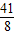
;
联立直线l和抛物线的解析式,得:
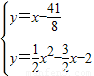
,
解得
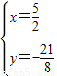
则P(

,-
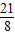
);
过P作PM⊥x轴于M,如图(2)②
△CDP的最大面积:Smax=

×(2+
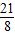
)×

-

×2×2-

×(

-2)×
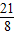
=
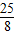
;
综上,当P(

,-
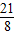
)时,△CDP的面积有最大值,且最大面积为
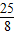
.
点评:此题主要考查的知识点有:一元二次方程的解法、利用待定系数法求函数的解析式、等腰三角形的判定、三角形面积的求法等;(2)的两个小题较为复杂,在①中,没有明确等腰三角形的底和腰是容易漏解的地方,这里需要分类讨论;在②中,此题所用的解法是平行法,也可直接用面积法来获取关于S
△CDP和m的函数关系式,但是必须根据P点的不同位置分段进行讨论,因为P点的位置直接影响到了面积间的和差关系.


 (x+1)(x-4)=
(x+1)(x-4)= x2-
x2- x-2.
x-2. x-2;
x-2; x-2=-
x-2=- ,即 E(3,-
,即 E(3,- );
);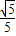 ,cos∠DBE=
,cos∠DBE=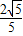 ;
;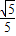 =
=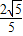 ,BF=BE•cos∠DBE=
,BF=BE•cos∠DBE=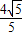 ,
,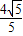 ,即 E(4-
,即 E(4-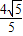 ,-
,-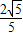 );
);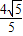 ,则 BE=2BH=
,则 BE=2BH=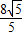 ;
;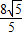 •
•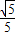 =
= ,BG=BE•cos∠DBE=
,BG=BE•cos∠DBE=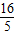 ,
, ,即 E(
,即 E( ,-
,- );
); );当BE=BD时,E(4-
);当BE=BD时,E(4-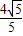 ,-
,-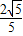 );当BD=DE时,E(
);当BD=DE时,E( ,-
,- ).
).


 ②由C(0,-2)、D(2,0)得,直线CD:y=x-2;
②由C(0,-2)、D(2,0)得,直线CD:y=x-2; x2-
x2- x-2,即:
x-2,即: x2-
x2- x-2-b=0
x-2-b=0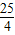 -4×
-4× ×(-2-b)=0,解得 b=-
×(-2-b)=0,解得 b=-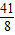
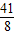 ;
;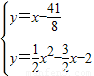 ,
,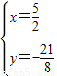
 ,-
,-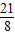 );
); ×(2+
×(2+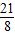 )×
)× -
- ×2×2-
×2×2- ×(
×( -2)×
-2)×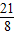 =
=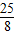 ;
; ,-
,-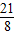 )时,△CDP的面积有最大值,且最大面积为
)时,△CDP的面积有最大值,且最大面积为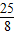 .
.

 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.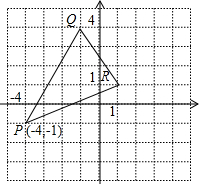 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示: