
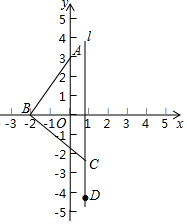 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$. 分析 如图,当点B从(-3,0)平移到(3,0)的过程中,C从C1(0,-3)运动到C2(6,3),D从D1(0,-6)→D2(3,0)→D3(6,0).求出D1D2=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,D2D3=3,即可解决问题.
解答 解:如图,当点B从(-3,0)平移到(3,0)的过程中,C从C1(0,-3)运动到C2(6,3),D从D1(0,-6)→D2(3,0)→D3(6,0).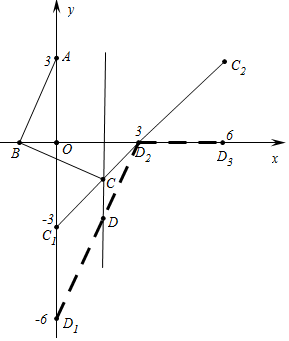
D1D2=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,D2D3=3,
∴点D的运动路径长为3+3$\sqrt{5}$,
故答案为3+3$\sqrt{5}$.
点评 本题考查坐标与图形的变化,旋转变换.平移变换等知识,解题的关键是正确寻找点D的运动轨迹,属于中考常考题型.


科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
一个数的平方根与立方根都是它本身,这个数是( )
A. 1 B. ﹣1 C. 0 D. ±1,0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?
如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
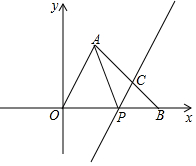 如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.
如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com