
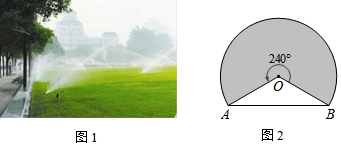
分析 作OC⊥AB,根据垂径定理得出AC=9,继而可得圆的半径OA的值,再根据扇形面积公式可得答案.
解答 解:过点O作OC⊥AB于C点.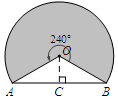
∵OC⊥AB,AB=18,
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×18=9(cm),
∵OA=OB,∠AOB=360°-240°=120°,
∴∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120=60°.
在Rt△OAC中,OA2=OC2+AC2,
又∵OC=$\frac{1}{2}$OA,
∴r=OA=6$\sqrt{3}$.
∴S=$\frac{240}{360}$πr2=72π(m2).
故答案是:72π.
点评 本题主要考查垂径定理和扇形的面积公式,熟练掌握垂径定理求得圆的半径是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
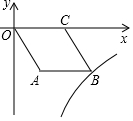 如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | -48 | B. | -64 | C. | -96 | D. | -128 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com