
����Ŀ�����壺���߳���������������������γ�Ϊ�����������Ρ��� ��ѧѧϰС���ͬѧ��32���ȳ��Ļ�����ÿ�����ȼ�Ϊ1����λ����ȡ�����ɸ�����β���������������Σ�����̽�����
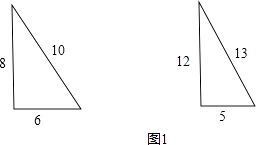
С����12���������ڳ���ͼ��ʾ�ġ����������Ρ���
Сӱ�ֱ���24����30�������ڳ�ֱ�ǡ����������Ρ���
С���ܵ�С����Сӱ���������ֱ�ڳ�������ͬ�ĵ��������������Ρ���
��1�����㻭��Сӱ��С�ڳ��ġ����������Ρ���ʾ��ͼ��
��2�����ܷ�Ҳ����ȡ�����ɸ���������Ҫ��ڳ������������Ρ�������ܣ��뻭��ʾ��ͼ��������ܣ���˵�����ɣ� �ٰڳ��ȱߡ����������Ρ���
�ڰڳ�һ�������⣨�ȷ�ֱ�������Σ�Ҳ�ǵ��������Σ������������Ρ���
���𰸡�
��1���⣺Сӱ�ڳ���ͼ1��ʾ�ġ����������Ρ���
С�ڳ���ͼ2��ʾ������ͬ�ĵ��������������Ρ���
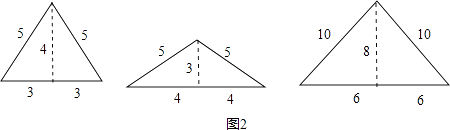
��2���⣺�ٲ��ܰڳ��ȱߡ����������Ρ���
�������£�
��ȱ������εı߳�Ϊa����ȱ����������Ϊ ![]() ��
��
��Ϊ�����߳�aΪ��������ô��� ![]() һ����������
һ����������
���Բ����ڵȱߡ����������Ρ���
���ܰڳ���ͼ3��ʾһ�������⡰���������Ρ���
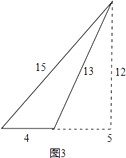
����������1�����ù��ɶ������6��8��10��5��12��13����Ҫ���ɵó��𰸣���2��������ȱ������εı߳�Ϊa����ȱ����������Ϊ ![]() ��������������ڵȱߡ����������Ρ���
��������������ڵȱߡ����������Ρ���


 �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ4a2b+3ab2��2b2+a3��a���������е��ǣ� ��
A.��2b3+3ab2+4a2b+a3
B.a3+4a2b+3ab2��2b3
C.4a2b+3ab2��2b3+a3
D.4a2b+3ab2+a3��2b3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ֪��AB ��y�ύ�ڵ�A����x�ύ�ڵ�B����˫����y= ![]() ��x��0�����ڵ�C��1��6���͵�D��3��n������CE��y����E��DF��x����F��
��x��0�����ڵ�C��1��6���͵�D��3��n������CE��y����E��DF��x����F��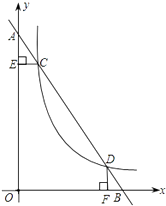
��1�����m��n��ֵ��
��2�����ֱ��AB�Ľ���ʽ��
��3���Ƿ��С�AEC�ա�DFB����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ�һֻ���ϴ�ԭ�������������������4����λ���ȵ����A��������������2����λ���ȵ����B��Ȼ��������������10����λ���ȵ����C��
��1���������������������ϱ�ʾ��A��B��C���㣻
��2�����ݵ�C�������ϵ�λ�ã���C���Կ��������ϴ�ԭ����������ĸ����������˼�����λ���ȵõ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С����������һ��С�γ�����������¼��7����ÿ����ʻ��·�̣����������50kmΪ��������50km�ļ�Ϊ��+��������50km�ļ�Ϊ���������պ�50km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·�̣�km�� | ��8 | ��11 | ��14 | 0 | ��16 | +41 | +8 |
��1�������������ƽ��ÿ����ʻ����ǧ�ף�
��2����ÿ��ʻ100km��������6�������ͼ�6.2Ԫ/���������С����һ���£���30��ƣ������ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1��С��������ɵ������У��ı���ABCD���ĸ����㶼�ڸ���ϣ��밴Ҫ��������и��⣮ 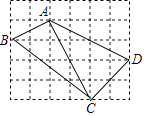
��1���߶�AB�ij�Ϊ �� BC�ij�Ϊ �� CD�ij�Ϊ��
��2������AC��ͨ������˵����ACD�͡�ABC��ʲô���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1����֪����ͼ�٣��ڡ�ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E����֤��DE=BD+CE�� 
��2����ͼ�ڣ�����1���е�������Ϊ���ڡ�ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=�������Ц�Ϊ����۽ǣ����ʽ���DE=BD+CE�Ƿ���������������������֤����������������˵�����ɣ� 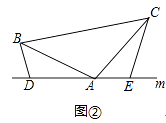
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com