
分析 首先设指导前平均每秒撤离的人数为x人,则经专家指导后,平均每秒撤离的人数是2x人,根据“这60名同学全部撤离的时间比指导前快30秒”可得等量关系:60人在被专家指导前撤离所用的时间-60人在被专家指导后撤离所用的时间=30秒,由等量关系列出方程,解方程即可.
解答 解:设指导前平均每秒撤离的人数为x人,由题意得:
$\frac{60}{x}$-$\frac{60}{2x}$=30,
解得:x=1,
经检验:x=1是原分式方程的解,
答:指导前平均每秒撤离的人数为1人.
点评 此题主要考查了分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.列分式方程解应用题的一般步骤:审、设、列、解、验、答.必须严格按照这6步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
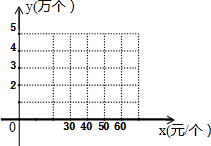 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两条边分别相等的两个等腰三角形全等 | |
| B. | 两腰对应相等的两个等腰三角形全等 | |
| C. | 有两条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一条直角边对应相等的两个直角三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
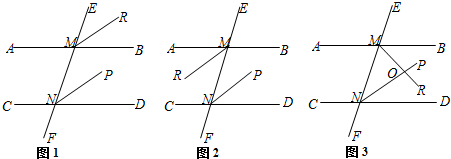
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
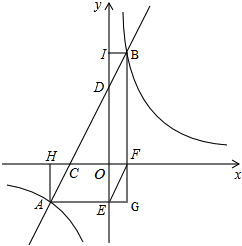 如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G.
如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com