
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
先由平行四边形的性质求得A的坐标,然后根据“关于![]() 轴轴对称的点,横坐标相同,纵坐标互为相反数”以及“关于
轴轴对称的点,横坐标相同,纵坐标互为相反数”以及“关于![]() 轴轴对称的点,纵坐标相同,横坐标互为相反数”求得每一次轴对称变换A的坐标,得出每4次轴对称变换为一个循环周期的规律,由此得出经过第2018次变换后,A点的坐标.
轴轴对称的点,纵坐标相同,横坐标互为相反数”求得每一次轴对称变换A的坐标,得出每4次轴对称变换为一个循环周期的规律,由此得出经过第2018次变换后,A点的坐标.
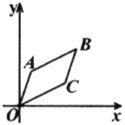
∵平行四边形OABC的顶点O(0,0),B(2,2),C(1.6,0.8)
∴A的横坐标为2-1.6=0.4,纵坐标为2-0.8=1.2,即A(0.4,1.2)
将平行四边形先沿着![]() 轴进行第一次轴对称变换,得A(-0.4,1.2);
轴进行第一次轴对称变换,得A(-0.4,1.2);
所得图形再沿着![]() 轴进行第二次轴对称变换,得A(-0.4,-1.2);
轴进行第二次轴对称变换,得A(-0.4,-1.2);
第三次轴对称变换,得A(0.4,-1.2);
第四次轴对称变换,得A(0.4,1.2),即A点回到原处.
由此可知,每4次轴对称变换为一个重复周期.
2018÷4=504……2
所以经过第2018次变换后,平行四边形顶点A位于第三象限,其坐标为(-0.4,-1.2).
故选:B.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
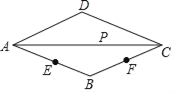
【题目】如图,四边形ABCD是菱形.AB=5,点P是对角线AC上任意一点,E、F分别是AB、BC边上的中点.当点P在线段AC上移动时,则PE+PF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
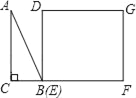
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. 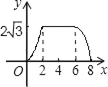 B.
B. 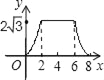 C.
C. 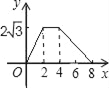 D.
D. 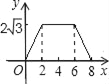
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索发现)
如图①,是一张直角三角形纸片,![]() ,小明想从中剪出一个以
,小明想从中剪出一个以![]() 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线
为内角且面积最大的矩形,经过多次操作发现,当沿着中位线![]() 、
、![]() 剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为_____________.
剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为_____________.
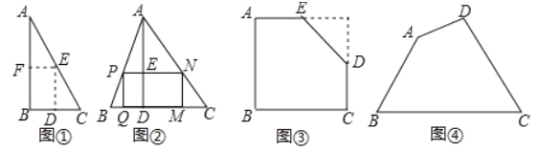
(拓展应用)
如图②,在![]() 中,
中,![]() ,
,![]() 边上的高
边上的高![]() ,矩形
,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 在边
在边![]() 上,则矩形
上,则矩形![]() 面积的最大值为_________.(用含
面积的最大值为_________.(用含![]() 的代数式表示)
的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明从中剪出了一个面积最大的矩形(
,小明从中剪出了一个面积最大的矩形(![]() 为所剪出矩形的内角),求该矩形的面积.
为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,木匠徐师傅从这块余料中裁出了顶点
,木匠徐师傅从这块余料中裁出了顶点![]() 、
、![]() 在边
在边![]() 上且面积最大的矩形
上且面积最大的矩形![]() ,求该矩形的面积.
,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在开业前,所进三种货物:上衣、裤子和鞋子的数量共480份,这三种货物进货的数量比例如图(1)所示.商店安排6人只销售上衣,4人只销售裤子,2人只销售鞋子,用了5天的时间销售货物的情况如图(2)及表格所示.
(1)求所进三种货物中上衣有多少件?
(2)直接在图中把图(2)补充完整;
(3)表格中的![]() = (直接填空);
= (直接填空);
(4)若销售人员不变,并以同样的销售速度销售,则上衣、裤子和鞋子中最先销售完的货物为 (直接填空).

货物 | 上衣(件) | 裤子(条) | 鞋子(双) |
5天的销售总额 | 150 | a | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是楼梯一部分示意图,楼梯台阶宽度均为![]() ,高度均为
,高度均为![]() ,且
,且![]() ,
,![]() 均与楼面垂直,点
均与楼面垂直,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
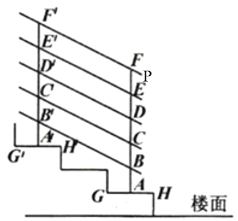
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求![]() 的值;
的值;
(3)求点![]() 到水平楼面的距离(精确到
到水平楼面的距离(精确到![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可以旋转,当
可以旋转,当![]() 绕点
绕点![]() 逆时针旋转时,投影探头
逆时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到
.(结果精确到![]() )
)
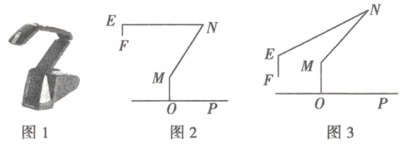
(1)如图2所示,![]() ,
,![]() .
.
①填空:![]() ;
;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离;
的距离;
(2)如图3所示,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据
的大小.(参考数据![]() span>)
span>)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,连结AC,CD.
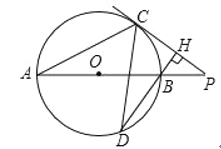
(1)求证:∠PBH=2∠HDC;
(2)若sin∠P=![]() ,BH=3,求BD的长.
,BH=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4.将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上.
(1)在下图所示的直角坐标系中,求E点的坐标及AE的长.
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标.
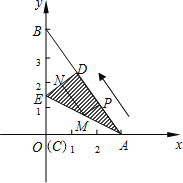
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com