
【题目】在平面直角坐标系中,已知抛物线![]() .
.
(1)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“方点”.试求拋物线![]() 的“方点”的坐标;
的“方点”的坐标;
(2)如图,若将该抛物线向左平移1个单位长度,新抛物线与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 左侧),与
左侧),与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() .若点
.若点![]() 是直线
是直线![]() 上方抛物线上的一点,求
上方抛物线上的一点,求![]() 的面积的最大值;
的面积的最大值;
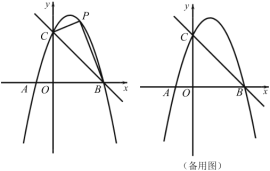
(3)第(2)问中平移后的抛物线上是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,直接写出所有符合条件的点
为直角边的直角三角形?若存在,直接写出所有符合条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)抛物线的方点坐标是![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)由定义得出x=y,直接代入求解即可
(2)作辅助线PD平行于y轴,先求出抛物线与直线的解析式,设出点P的坐标,利用点坐标求出PD的长,进而求出面积的二次函数,再利用配方法得出最大值
(3)通过抛物线与直线的解析式可求出点B,C的坐标,得出△OBC为等腰直角三角形,过点C作![]() 交x轴于点M,作
交x轴于点M,作![]() 交y轴于点N,得出M,N的坐标,得出直线BN、MC的解析式然后解方程组即可.
交y轴于点N,得出M,N的坐标,得出直线BN、MC的解析式然后解方程组即可.
解:(1)由题意得:![]() ∴
∴![]()
解得![]() ,
,![]()
∴抛物线的方点坐标是![]() ,
,![]() .
.
(2)过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() .
.
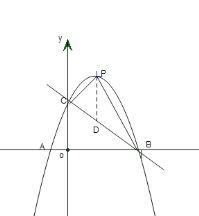
易得平移后抛物线的表达式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() .
.
设![]() ,则
,则![]() .
.
∴![]()
![]()
∴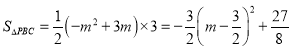
![]()
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
(3)如图所示,过点C作![]() 交x轴于点M,作
交x轴于点M,作![]() 交y轴于点N
交y轴于点N
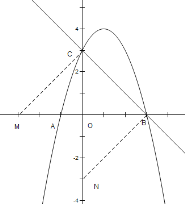
由已知条件得出点B的坐标为B(3,0),C的坐标为C(0,3),
∴△COB是等腰直角三角形,
∴可得出M、N的坐标分别为:M(-3,0),N(0,-3)
直线CM的解析式为:y=x+3
直线BN的解析式为:y=x-3
由此可得出: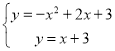 或
或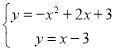
解方程组得出:![]() 或
或![]()
∴![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
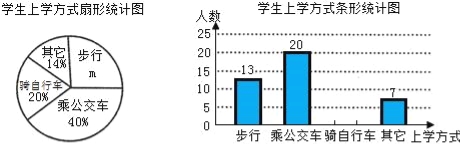
(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)
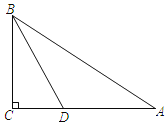
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 网络比
网络比![]() 网络的传输速度快10倍以上,因此人们对
网络的传输速度快10倍以上,因此人们对![]() 产品充满期待.华为集团计划2020年元月开始销售一款
产品充满期待.华为集团计划2020年元月开始销售一款![]() 产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第
产品.根据市场营销部的规划,该产品的销售价格将随销售月份的变化而变化.若该产品第![]() 个月(
个月(![]() 为正整数)销售价格为
为正整数)销售价格为![]() 元/台,
元/台,![]() 与
与![]() 满足如图所示的一次函数关系:且第
满足如图所示的一次函数关系:且第![]() 个月的销售数量
个月的销售数量![]() (万台)与
(万台)与![]() 的关系为
的关系为![]() .
.
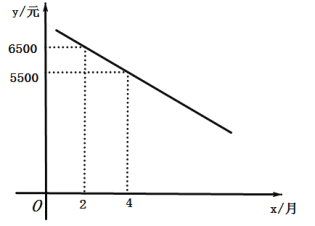
(1)该产品第6个月每台销售价格为______元;
(2)求该产品第几个月的销售额最大?该月的销售价格是多少元/台?
(3)若华为董事会要求销售该产品的月销售额不低于27500万元,则预计销售部符合销售要求的是哪几个月?
(4)若每销售1万台该产品需要在销售额中扣除![]() 元推广费用,当
元推广费用,当![]() 时销售利润最大值为22500万元时,求
时销售利润最大值为22500万元时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系x0y中,对于图形G,若存在一个正方形γ,这个正方形的某条边与x轴垂直,且图形G上的所有的点都在该正方形的内部或者边上,则称该正方形γ为图形G的一个正覆盖.很显然,如果图形G存在一个正覆盖,则它的正覆盖有无数个,我们将图形G的所有正覆盖中边长最小的一个,称为它的紧覆盖.如图所示,图形G为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形G的正覆盖,其中正方形ABCD就是图形G的紧覆盖.

(1)对于半径为2的⊙0,它的紧覆盖的边长为 .
(2)如图1,点P为直线y=-2x+3上一动点,若线段OP的紧覆盖的边长为2,求点P的坐标;
(3)如图2,直线y=3x+3与x轴,y轴分别交于A,B,
①以0为圆心,r为半径的⊙0与线段AB有公共点,且由⊙0与线段AB组成的图形G的紧覆盖的边长小于4,直接写出r的取值范围;
②若在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆盖的边长为3,直接写出a的取值范围.
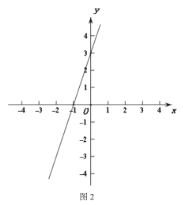
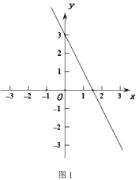
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
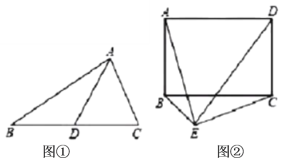
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com