
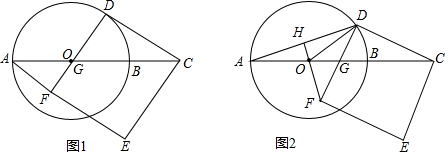
分析 (1)在Rt△ODC中,求出∠ACD的值即可解决问题.
(2)①设OG=GB=a,则OB=BC=OD=2a,可知OD2=OG•OC=4a2,推出$\frac{OD}{OG}$=$\frac{OC}{OD}$,由∠DOG=∠COD,即可证明△DOG∽△COD.
②连接BD,作GM⊥AD于M,GN⊥DB于N.只要证明∠BDG=∠CDB=∠ADG,由GM⊥AD,GN⊥DB,推出GM=GN,可知S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,推出tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$即可.
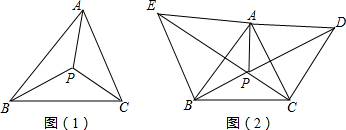
解答 (1)解:如图1中,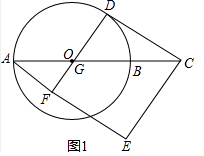
∵四边形EFDC是正方形,
∴∠ODC=90°,
∵OB=BC=OD,
∴OC=2OD,
∴sin∠ACD=$\frac{OD}{OC}$=$\frac{1}{2}$,
∴∠ACD=30°.
(2)解:如图2中,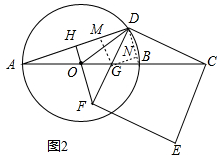
①证明:设OG=GB=a,则OB=BC=OD=2a,
∴OD2=OG•OC=4a2,
∴$\frac{OD}{OG}$=$\frac{OC}{OD}$,∵∠DOG=∠COD,
∴△DOG∽△COD.
②连接BD,作GM⊥AD于M,GN⊥DB于N.
∵AB是直径,
∴∠ADB=∠GDC=90°,
∴∠ADG=∠CDB,
∵△DOG∽△COD,
∴∠ODG=∠DCB,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠ODG+∠BDG=∠BDC+∠DCB,
∴∠BDG=∠CDB=∠ADG,
∵GM⊥AD,GN⊥DB,
∴GM=GN,
∵S△ADG:S△DGB=$\frac{1}{2}$AD•GM:$\frac{1}{2}$•DB•GN=AD+DB=AG:GB=3:1,
∴$\frac{DB}{AD}$=$\frac{1}{3}$,
∴tan∠DAC=$\frac{DB}{AD}$=$\frac{1}{3}$.
点评 本题考查相似三角形的判定和性质、正方形的性质、解直角三角形、圆周角定理、勾股定理等知识,解题的关键是学会利用参数解决问题,本题体现了数形结合的数学思想,学会添加常用辅助线,掌握用面积法证明线段之间的关系,属于中考压轴题.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
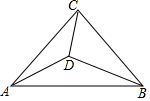 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.
如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
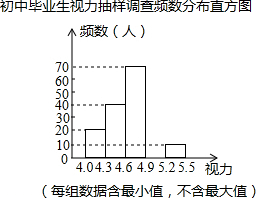 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com