
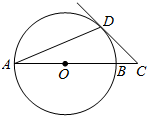
 如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°,
如图,AB是⊙O的直径,AD是弦,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°, 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
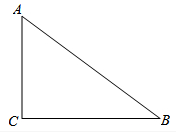 如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.
如图,已知Rt△ABC中,∠ACB=90°.请完成以下任务.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )| A. | $\frac{5}{12}$π | B. | π | C. | $\frac{5}{3}$π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+5)=150 | B. | x(x-5)=150 | C. | (x+5)(x-5)=150 | D. | (x+5)2=150 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
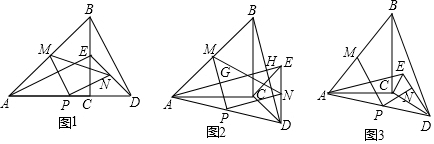
 如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )
实数a,b在数轴上的对应点的位置如图所示,把a,-b,0按照从小到大的顺序排列,正确的是( )| A. | a<0<-b | B. | 0<a<-b | C. | -b<0<a | D. | -b<a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
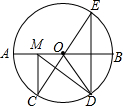 如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
如图,在⊙O中,AB是⊙O的直径,AB=10,$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=$\frac{1}{2}$∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com