
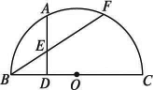
如图,已知BC为半圆O的直径,![]() =
=![]() ,AC交BF于点M,过A作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
,AC交BF于点M,过A作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?

|
[答案]相等.理由如下: 解法 1:如图,∵BC是直径,
∴∠ BAC=∵ AD⊥BC,∴∠ABD+∠BAD=∴∠ BAD=∠ACB.∵∴∠ ABF=∠ACB,即∠ABE=∠ACB.∴∠ ABE=∠BAD.∴AE=BE.解法 2:如图连接OA、OF设OA交BF于点G,则
∵ ∴ AO⊥BF,即∠AGB=∵∠ ADB=∵ OB=OA,∴∠OBA=∠OAB.∴∠ OBA-∠EBD=∠OAB-∠EAG,即∠ABE=∠BAE.∴AE=BE.解法 3:如图,作出⊙O,延长AD交⊙O于H,则
∵ AH⊥BC,BC为直径.∴∴ ∴ AE=BE.[剖析]要证明AE=BE,则需证明∠ABE=∠BAE,观察图形可知∠ACB=∠ABE,于是转证∠ACB=∠BAE即可,由此得到解法1,由已知可得点A平分 |
|
[方法提炼] 要证圆周角相等,可证它们所对的弧相等,或证明它们都与第三个角相等,或通过全等 (或其他方法)来证.在圆中,可通过垂径定理、圆周角的性质等得到相等的弧、直角等.另外同一个圆中的任意两条半径可作为某一等腰三角形的腰. |


科目:初中数学 来源:1课3练 单元达标测试八年级数学(下) 国标人教版 题型:044
如图,已知△ABC为直角三角形,∠C=![]() ,分别以AB、AC、BC为直径向外作半圆,试说明三个半圆的面积之间的关系,并说明理由.
,分别以AB、AC、BC为直径向外作半圆,试说明三个半圆的面积之间的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源:课堂三级讲练数学九年级(上) 题型:044
1.已知如图所示,BC为半圆O的直径,AB⊥BC,垂足为D,过点B作弦BF交AD于点E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,求证:(1)![]() =
=![]() ;(2)AH·BC=2AB·BE.
;(2)AH·BC=2AB·BE.

2.在上题中若加上条件sin∠FBC=![]() ,AB=4
,AB=4![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源:设计九年级上数学人教版 人教版 题型:047
如图,已知BC为半圆O的直径,F是半圆上异于B、C的一点,A是![]() 的中点,AD⊥BC于点D,BF交AD于点E.
的中点,AD⊥BC于点D,BF交AD于点E.
(1)求证:BE·BF=BD·BC;
(2)试比较线段BD与AE的大小,并说明道理.
查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:047
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com