
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
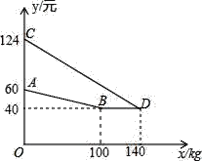
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
【答案】(1)点D的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元;(2)y2=﹣![]() x+124(0≤x≤140); (3)当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.
x+124(0≤x≤140); (3)当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.
【解析】
(1)点D的横坐标、纵坐标的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元.
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可.
(3)先求出销售价![]() 与产量x之间的函数关系,利用:总利润=每千克利润×产量列出有关x的一次函数,求得最值即可.
与产量x之间的函数关系,利用:总利润=每千克利润×产量列出有关x的一次函数,求得最值即可.
解:(1)点D的实际意义:当产量为140kg时,该产品每千克生产成本与销售价相等,都为40元.
(2)设线段CD所表示的y2与x之间的函数表达式为y2=k1x+b1,
∵点(0,124),(140,40)在函数y2=k1x+b1的图象上,
∴y2与x之间的函数表达式为y2=﹣![]() x+124(0≤x≤140);
x+124(0≤x≤140);
(3)设线段AB所表示的y1与x之间的函数表达式为y1=k2x+b2,
∵点(0,60),(100,40)在函数y1=k2x+b2的图象上,
∴y1与x之间的函数表达式为y1=﹣![]() x+60(0≤x≤100)
x+60(0≤x≤100)
设产量为x千克时,获得的利润为W元.
①当0≤x≤100时,W=[(﹣![]() x+124)﹣(﹣
x+124)﹣(﹣![]() x+60)]x=﹣
x+60)]x=﹣![]() (x﹣80)2+2560,
(x﹣80)2+2560,
∴当x=80时,W的值最大,最大值为2560元.
②当100≤x≤140时,W=[(﹣![]() x+124)﹣40]x=﹣
x+124)﹣40]x=﹣![]() (x﹣70)2+2940, 由﹣
(x﹣70)2+2940, 由﹣![]() <0知,
<0知,
当x≥70时,W随x的增大而减小,
∴当x=100时,W的值最大,最大值为2400元.
∵2560>2400,
∴当该产品的质量为80kg时,获得的利润最大,最大利润为2560元.


科目:初中数学 来源: 题型:
【题目】
(已有经验)
我们已经研究过作一个圆经过两个已知点,也研究过作一个圆与已知角的两条边都相切,尺规作图如图所示:
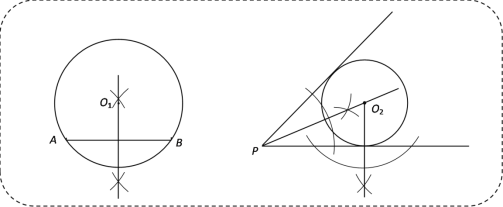
(迁移经验)
(1)如图①,已知点M和直线l,用两种不同的方法完成尺规作图:求作⊙O,使⊙O过M点,且与直线l相切.(每种方法作出一个圆即可,保留作图痕迹,不写作法)

(问题解决)
如图②,在Rt△ABC中,∠C=90°,AC=8,BC=6.
(2)已知⊙O经过点C,且与直线AB相切.若圆心O在△ABC的内部,则⊙O半径r的取值范围为 .
(3)点D是边AB上一点,BD=m,请直接写出边AC上使得∠BED为直角时点E的个数及相应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)求抛物线的对称轴;
(2)当![]() 时,设抛物线与
时,设抛物线与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),顶点为
左侧),顶点为![]() ,若
,若![]() 为等边三角形,求
为等边三角形,求![]() 的值;
的值;
(3)过![]() (其中
(其中![]() )且垂直
)且垂直![]() 轴的直线
轴的直线![]() 与抛物线交于
与抛物线交于![]() 两点.若对于满足条件的任意
两点.若对于满足条件的任意![]() 值,线段
值,线段![]() 的长都不小于1,结合函数图象,直接写出
的长都不小于1,结合函数图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于点A(-2,0)、B(4,0),与y轴相交于点C,连接BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E.
与x轴相交于点A(-2,0)、B(4,0),与y轴相交于点C,连接BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E.
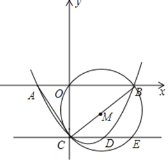
(1)求该抛物线所对应的函数关系式;
(2)求线段DE的长;
(3)在BC下方的抛物线上有一点P,P点的横坐标是m,△PBC的面积为S,求出S与m之间的函数关系式,并求出当m为何值时,S有最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘中各个扇形的面积相等,分别标有数字1,2,3,4,小兰转动转盘,记下指针所在扇形内的数字为![]() ,再由小田转动转盘,记下指针所在扇形内的数字为
,再由小田转动转盘,记下指针所在扇形内的数字为![]() ,将
,将![]() 和
和![]() 分别作为点的横坐标和纵坐标,得到点
分别作为点的横坐标和纵坐标,得到点![]()

(1) 用列表法或画树状图法表示出![]() 的所有等可能出现的结果;
的所有等可能出现的结果;
(2) 求点![]() 落在一次函数
落在一次函数![]() 的图象上的概率;
的图象上的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com