
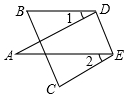
 如图所示,将纸片△ABC沿着DE折叠压平,则∠A,∠1与∠2之间的数量关系是∠A=$\frac{1}{2}$(∠1+∠2).
如图所示,将纸片△ABC沿着DE折叠压平,则∠A,∠1与∠2之间的数量关系是∠A=$\frac{1}{2}$(∠1+∠2). 分析 由折叠及邻补角的性质可知,∠1=180°-2∠ADE,∠2=180°-2∠AED,两式相加,结合已知可求∠ADE+∠AED的度数,在△ADE中,由内角和定理可求∠A的度数.
解答 解:根据折叠及邻补角的性质,得
∠1=180°-2∠ADE,∠2=180°-2∠AED,
∴∠1+∠2=360°-2(∠ADE+∠AED),
∴∠ADE+∠AED=$\frac{1}{2}$[360°-(∠1+∠2)]=180°-$\frac{1}{2}$(∠1+∠2),
∴在△ADE中,由内角和定理,得
∠A=180°-(∠ADE+∠AED)=180°-180°+$\frac{1}{2}$(∠1+∠2)=$\frac{1}{2}$(∠1+∠2).
故答案为:∠A=$\frac{1}{2}$(∠1+∠2).
点评 本题考查了折叠的性质,邻补角的性质,三角形内角和定理,关键是把∠1+∠2看作整体,对角的和进行转化.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN.
如图,AC分别切⊙O于D、E,作OQ⊥BC交⊙O于P,连DP、EP交BC于G、F,AF、AG分别交DG、EF于M、N.求证:OQ⊥MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.
如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
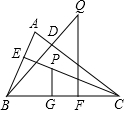 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com