
����Ŀ����ͼ���ı���![]() �У���
�У���![]() Ϊֱ������ϵ��ԭ�㣬
Ϊֱ������ϵ��ԭ�㣬![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() ͬʱ��ԭ��������ֱ��������˶�����
ͬʱ��ԭ��������ֱ��������˶�����![]() ��
��![]() ��ÿ��1����λ���յ�
��ÿ��1����λ���յ�![]() �˶�����
�˶�����![]() ��
��![]() ��ÿ��2����λ���յ�
��ÿ��2����λ���յ�![]() �˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ
�˶���������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮

��1������![]() ��ʾ��
��ʾ��![]() ������Ϊ__________��
������Ϊ__________��
��2���Ƿ����ij��ʱ��![]() ��ʹ���Ե�
��ʹ���Ե�![]() ���ı���
���ı���![]() �е�������������Ϊ������ı���Ϊƽ���ı��Σ������ڣ������
�е�������������Ϊ������ı���Ϊƽ���ı��Σ������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ��ֵΪ6��
��ֵΪ6��![]() ��
��
��������
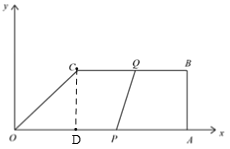
��1������A��B��C������������OA��AB��BC�ij�������C��CD��OA�����ı���CDAB�Ǿ��Σ����ù��ɶ��������OC�ij������þ���=�ٶ���ʱ�伴�ɵô𰸣�
��2����P��Q����ֱ���O��C��A��B��P��Q��C��A�������������ƽ���ı��ε����ʷֱ����tֵ������t��9����Q����λ���жϼ��ɵô𰸣�
��1����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��
��OA=16��AB=6��BC=8��
����C��CD��OA�����ı���CDAB�Ǿ��Σ�
��CD=AB=6��OD=OA-BC=8��
��![]() ����ʱ��
����ʱ��![]() ��s����
��s����
�ߵ�Q���ٶ�Ϊÿ��2����λ��
�൱![]() ʱ��
ʱ��![]() ����ʱ��
����ʱ��![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��
���Q�ĺ�����ΪOD+CQ=2t-10+8=2t-2��������Ϊ6��
��Q������Ϊ![]() ��
��
�ʴ�Ϊ����2t-2��6��
��2���ٵ�P��Q��O��C����ƽ���ı���ʱ����OP=CQ��
�ߵ�P�ٶ�Ϊÿ��1����λ��
��OP=t��
��CQ=2t-10��
��![]() ��
��
��ã�![]() ��
��![]() ì�ܣ��ᣩ��
ì�ܣ��ᣩ��
��P��Q��A��B����ƽ���ı���ʱ����PA=QB��
��OC=10��BC=8��
��QB=18-2t��
��PA=16-t��
��![]() ��
��
��ã�![]() ����ʱ
����ʱ![]() ��
��![]() �ϣ����������⣬��ȥ
�ϣ����������⣬��ȥ
�۵�P��Q��O��B����ƽ���ı���ʱ����OP=QB��
��OP=t��QB=18-2t��
![]() ��
��
��ã�![]() ���������⣬
���������⣬
��P��Q��C��A����ƽ���ı���ʱ����PA=CQ��
��PA=16-t��CQ=2t-10��
��![]() ��
��
���![]() ���������⣬
���������⣬
����������![]() ��ֵΪ6��
��ֵΪ6��![]() ��
��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ǰ����������![]() ����ʻ����Сʱ��;���ڼ���վ������������������������
����ʻ����Сʱ��;���ڼ���վ������������������������![]() (
(![]() )����ʻʱ��
)����ʻʱ��![]() (
(![]() )֮��ĺ�����ϵ��ͼ��ʾ������ͼ�ش�����:
)֮��ĺ�����ϵ��ͼ��ʾ������ͼ�ش�����:

��1����������ʻ![]() ����ͣ�;�м��� ��:
����ͣ�;�м��� ��:
��2������ͼ�μ��㣬�������ڼ���ǰ����ʻ��ÿСʱ���Ͷ�������
��3���������վ��Ŀ�ĵػ���![]() ������Ϊ
������Ϊ![]() ��Ҫ����Ŀ�ĵأ������е����Ƿ��ã���˵�����ɣ�
��Ҫ����Ŀ�ĵأ������е����Ƿ��ã���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AB��CD��ֱ��a��AB��CD�ֱ��ڵ�E��F����M��EF�ϣ�P��ֱ��CD�ϵ�һ�����㣬����P����F�غϣ�
��1������P������FC���ƶ�ʱ����FMP+��FPM =��AEF��������˵�����ɡ�
��2������P������FD���ƶ�ʱ����FMP+��FPM����AEF��ʲô��ϵ����˵���������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��������߳�Ϊ1��С�����ηֱ��ضԽ�������ƴ��������ABCD��
��1��������ABCD�����Ϊ�����������߳�Ϊ�����������Խ���BD=����������
��2����֤��![]() ��
��
��3����ͼ�ڣ���������ABCD���������ϣ�ʹ��B��ԭ��O�غϣ���AB����x��ĸ������ϣ����A����ʾ����Ϊ��������������E����ʾ����Ϊ���������E����ʾ����Ϊ����������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2��m+1��x+m2+2=0
��1����������ʵ��������ʵ��m��ȡֵ��Χ��
��2����������ʵ�����ֱ�Ϊx1��x2 �� ������x12+x22=10����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ״����Ҵ�Ĺ�·����һ��ɽ�����ڿ���������һ![]() ����Ҫ���ƣ���֪��
����Ҫ���ƣ���֪��![]() �빫·�ϵ�ͣ��վ
�빫·�ϵ�ͣ��վ![]() �ľ���Ϊ300�ף��빫·�ϵ���һͣ��վ
�ľ���Ϊ300�ף��빫·�ϵ���һͣ��վ![]() �ľ���Ϊ400�ף���
�ľ���Ϊ400�ף���![]() ����ͼ��ʾΪ�˰�ȫ��������Ƶ�
����ͼ��ʾΪ�˰�ȫ��������Ƶ�![]() ��Χ�뾶250��Χ�ڲ��ý��룬���ڽ��б���ʱ����·
��Χ�뾶250��Χ�ڲ��ý��룬���ڽ��б���ʱ����·![]() ���Ƿ���Ϊ��Σ�ն���Ҫ��ʱ��������˵�����ɣ�
���Ƿ���Ϊ��Σ�ն���Ҫ��ʱ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ�ཻ�ڵ�D������BD��BE��CE������CBD=32�㣬���BEC�Ķ���Ϊ�� ��
A.128��
B.126��
C.122��
D.120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ�����������̣�
��ͼ����֪AB��CE����A����E����˵������CGD����FHB.

�⣺��ΪAB��CE(��֪)��
���ԡ�A���� ( )��
��Ϊ��A����E(��֪)��
���ԡ� ���� (��������)��
���� �� ( )��
���ԡ�CGD���� ( )��
����FHB����GHE( )��
���ԡ�CGD����FHB(��������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽⡰�γ�ѡ�ޡ���������Ա����μӡ��������͡������Ƽ�������������ѧ˼ά�������Ķ�д�������ĸ�ѡ����Ŀ��ѧ����ÿ���ޱ�һ����г������飬�����Ǹ����ռ������ݻ��Ƶ�������������ͳ��ͼ��
����ͼ���ṩ����Ϣ������������⣺
��1���˴ι���������ѧ��������ͳ��ͼ�У����������͡�����Ӧ��Բ�ĽǵĶ������ȣ�
��2������������ͳ��ͼ����������
��3���ָ�У700��ѧ�������μ����ĸ�ѡ����Ŀ����������ж�����ѧ���μ��ˡ���ѧ˼ά����Ŀ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com