
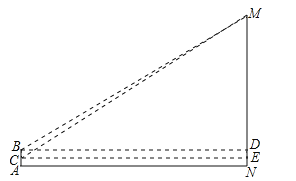
”¾ĢāÄæ”æijŹŠŅ»ŗžµÄŗžŠÄµŗÓŠŅ»æÅ°ŁÄź¹ÅŹ÷£¬µ±µŲČĖ³ĘĖüĪŖ”°ĻēĖ¼Įų”±£¬²»³Ė“¬²»Ņ×µ½“ļ£¬ĆæÄź³õ“ŗŹ±½Ś£¬ČĖĆĒĻ²»¶ŌŚ”°¾ŪĻĶĶ¤”±¹ŪŗžÉĶĮų£®Š”ŗģŗĶŠ”¾üŗÜĻėÖŖµĄ”°¾ŪĻĶĶ¤”±Óė”°ĻēĖ¼Įų”±Ö®¼äµÄ“óÖĀ¾ąĄė£¬ÓŚŹĒ£¬ÓŠŅ»Ģģ£¬ĖūĆĒĮ©“ų×ŲąĒćĘ÷ŗĶʤ³ßĄ“²āĮæÕāøö¾ąĄė£®²āĮæ·½·ØČēĻĀ£ŗČēĶ¼£¬Ź×ĻČ£¬Š”¾üÕ¾ŌŚ”°¾ŪĻĶĶ¤”±µÄA“¦£¬ÓĆ²ąĒćĘ÷²āµĆ”°ĻēĖ¼Įų”±¶„¶ĖMµćµÄŃö½ĒĪŖ23”ć£¬“ĖŹ±²āµĆŠ”¾üµÄŃŪ¾¦¾ąµŲĆęµÄø߶ČABĪŖ1.7Ć×£¬Č»ŗ󣬊”¾üŌŚA“¦¶×ĻĀ£¬ÓĆ²ąĒćĘ÷²āµĆ”°ĻēĖ¼Įų”±¶„¶ĖMµćµÄŃö½ĒĪŖ24”ć£¬ÕāŹ±²āµĆŠ”¾üµÄŃŪ¾¦¾ąµŲĆęµÄø߶ČACĪŖ1Ć×£®ĒėÄćĄūÓĆŅŌÉĻ²āµĆµÄŹż¾Ż£¬¼ĘĖć”°¾ŪĻĶĶ¤”±Óė”°ĻēĖ¼Įų”±Ö®¼äµÄ¾ąĄėANµÄ³¤£Ø½į¹ū¾«Č·µ½1Ć×£©£®£Ø²Īæ¼Źż¾Ż£ŗsin23”ć”Ö0.3907£¬cos23”ć”Ö0.9205£¬tan23”ć”Ö0.4245£¬sin24”ć”Ö0.4067£¬cos24”ć”Ö0.9135£¬tan24”ć”Ö0.4452£®£©
”¾“š°ø”æ34Ć×£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ×÷BD”ĶMN£¬CE”ĶMN£¬“¹×ć·Ö±šĪŖµćD”¢E£¬ÉčAN=xĆ×£¬ŌņBD=CE=xĆ×£¬ŌŁÓÉČń½ĒČż½ĒŗÆŹżµÄ¶ØŅ弓æÉµĆ³ö½įĀŪ£®
ŹŌĢā½āĪö£ŗČēĶ¼£¬×÷BD”ĶMN£¬CE”ĶMN£¬“¹×ć·Ö±šĪŖµćD”¢E£¬ÉčAN=xĆ×£¬ŌņBD=CE=xĆ×£¬ŌŚRt”÷MBDÖŠ£¬MD=xtan23”ć£¬ŌŚRt”÷MCEÖŠ£¬ME=xtan24”ć£¬”ßME©MD=DE=BC£¬”ąxtan24”ć©xtan23”ć=1.7©1£¬”ąx=![]() £¬½āµĆx”Ö34£ØĆ×£©£®
£¬½āµĆx”Ö34£ØĆ×£©£®
“š£ŗ”°¾ŪĻĶĶ¤”±Óė”°ĻēĖ¼Įų”±Ö®¼äµÄ¾ąĄėANµÄ³¤Ō¼ĪŖ34Ć×£®




| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉč”÷ABCµÄĆ껿ĪŖ1£®
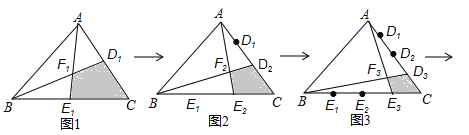
ČēĶ¼1£¬·Ö±š½«AC£¬BC±ß2µČ·Ö£¬D1£¬E1ŹĒĘä·Öµć£¬Į¬½ÓAE1£¬BD1½»ÓŚµćF1£¬µĆµ½ĖıߊĪCD1F1E1£¬ĘäĆ껿S1=![]() £®
£®
ČēĶ¼2£¬·Ö±š½«AC£¬BC±ß3µČ·Ö£¬D1£¬D2£¬E1£¬E2ŹĒĘä·Öµć£¬Į¬½ÓAE2£¬BD2½»ÓŚµćF2£¬µĆµ½ĖıߊĪCD2F2E2£¬ĘäĆ껿S2=![]() £»
£»
ČēĶ¼3£¬·Ö±š½«AC£¬BC±ß4µČ·Ö£¬D1£¬D2£¬D3£¬E1£¬E2£¬E3ŹĒĘä·Öµć£¬Į¬½ÓAE3£¬BD3½»ÓŚµćF3£¬µĆµ½ĖıߊĪCD3F3E3£¬ĘäĆ껿S3=![]() £»
£»
”
°“ÕÕÕāøö¹ęĀɽųŠŠĻĀČ„£¬Čō·Ö±š½«AC£¬BC±ß£Øn+1£©µČ·Ö£¬”£¬µĆµ½ĖıߊĪCDnEnFn£¬ĘäĆ껿S= £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°“ŗÖÖŅ»Į£ĖŚ£¬ĒļŹÕĶņæÅ×Ó”±£¬ĢĘ“śŹ«ČĖĄīÉšÕā¾äŹ«ÖŠµÄ”°ĖŚ”±¼“¹Č×Ó£ØȄʤŗóŌņ³ĘĪŖ”°Š”Ć×”±£©£¬±»ÓžĪŖÖŠ»ŖĆń×åµÄ²øÓż×÷Īļ£®ĪŅŹ”ÓŠ×Å”°Š”ŌÓĮøĶõ¹ś”±µÄĆĄÓž£¬¹Č×Ó×÷ĪŖĪŅŹ”ŌÓĮøĆ껿ĪŖ2000ĶņĶ£¬Äź×ܲśĮæĪŖ150Ķņ¶Ö£¬ĪŅŹ”¹Č×ÓĘ½¾łÄ¶²śĮæĪŖ160kg£¬¹śÄŚĘäĖūµŲĒų¹Č×ÓµÄĘ½¾łÄ¶²śĮæĪŖ60kg£®Ēė½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø1£©ĒóĪŅŹ”2016Äź¹Č×ÓµÄÖÖÖ²Ć껿ŹĒ¶ąÉŁĶņĶ£®
£Ø2£©2017Äź£¬ČōĪŅŹ”¹Č×ÓµÄĘ½¾łÄ¶²śĮæČŌ±£³Ö160kg²»±ä£¬ŅŖŹ¹ĪŅŹ”¹Č×ÓµÄÄź×ܲśĮæ²»µĶÓŚ52Ķņ¶Ö£¬ÄĒĆ“£¬½ńÄźĪŅŹ”ÖĮÉŁÓ¦ŌŁ¶ąÖÖÖ²¶ąÉŁĶņĶµÄ¹Č×Ó£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”泤¶Č·Ö±šĪŖ3cm£¬5cm£¬7cm£¬9cmµÄĖÄøłÄ¾°ō£¬ÄÜ“ī³É£ØŹ×Ī²Į¬½į£©Čż½ĒŠĪµÄøöŹżĪŖ£Ø £©
A. 1 B. 2 C. 3 D. 4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŃų³ÉĮ¼ŗƵÄŌē¶ĶĮ¶Ļ°¹ß£¬¶ŌѧɜµÄѧĻ°ŗĶÉś»ī¶¼·Ē³£ÓŠŅę£¬Ä³ÖŠŃ§ĪŖĮĖĮĖ½āĘßÄź¼¶Ń§ÉśµÄŌē¶ĶĮ¶Ēéæö£¬Š£Õž½Ģ“¦ŌŚĘßÄź¼¶Ė껜³éČ”ĮĖ²æ·Öѧɜ£¬²¢¶ŌÕāŠ©Ń§ÉśĶس£ĒéæöĻĀŅ»ĢģµÄŌē¶ĶĮ¶Ź±¼äx£Ø·ÖÖÓ£©½ųŠŠĮĖµ÷²é£®Ļְѵ÷²é½į¹ū·Ö³ÉA”¢B”¢C”¢DĖÄ×飬ČēĻĀ±ķĖłŹ¾£¬Ķ¬Ź±£¬½«µ÷²é½į¹ū»ęÖĘ³ÉĻĀĆęĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®

ĒėÄćøł¾ŻŅŌÉĻĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£»
£Ø2£©Ėł³éČ”µÄĘßÄź¼¶Ń§ÉśŌē¶ĶĮ¶Ź±¼äµÄÖŠĪ»ŹżĀäŌŚ Ēų¼äÄŚ£»
£Ø3£©ŅŃÖŖøĆŠ£ĘßÄź¼¶¹²ÓŠ1200Ćūѧɜ£¬ĒėÄć¹Ą¼ĘÕāøöÄź¼¶Ń§ÉśÖŠŌ¼ÓŠ¶ąÉŁČĖŅ»ĢģŌē¶ĶĮ¶µÄŹ±¼ä²»ÉŁÓŚ20·ÖÖÓ£®£ØŌē¶ĶĮ¶£ŗÖøѧɜŌŚŌē³æ7£ŗ00”«7£ŗ40Ö®¼äµÄ¶ĶĮ¶£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·Ø²»ÕżČ·µÄŹĒ£Ø £©
A. µČŃüČż½ĒŠĪŹĒÖį¶Ō³ĘĶ¼ŠĪ
B. Čż½ĒĻąµČµÄČż½ĒŠĪŹĒµČ±ßČż½ĒŠĪ
C. Čē¹ūĮ½øöČż½ĒŠĪ³ÉÖį¶Ō³Ę£¬ÄĒĆ“ÕāĮ½øöČż½ĒŠĪŅ»¶ØČ«µČ
D. ČōA,BĮ½µć¹ŲÓŚÖ±ĻßMN¶Ō³Ę£¬ŌņAB“¹Ö±Ę½·ÖMN
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠø÷Ź½“Ó×óµ½ÓŅµÄ±äŠĪ£¬ŹĒŅņŹ½·Ö½āµÄŹĒ£Ø £©
A.x2©9+6x=£Øx+3£©£Øx©3£©+6x
B.x2©8x+16=£Øx©4£©2
C.£Øx+5£©£Øx©2£©=x2+3x©10
D.6ab=2a3b
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄą±Č”¢×Ŗ»Æ”¢“ÓĢŲŹāµ½Ņ»°ćµČĖ¼Ļė·½·Ø£¬ŌŚŹżŃ§Ń§Ļ°ŗĶŃŠ¾æÖŠ¾³£ÓƵ½£¬Ēėæ“ĻĀĆęµÄ°øĄż£®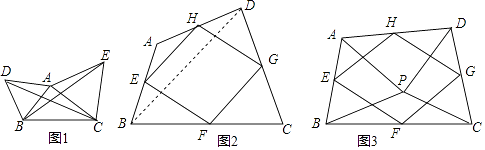
£Ø1£©ČēĶ¼1£¬ŅŃÖŖ”÷ABC£¬·Ö±šŅŌAB”¢ACĪŖ±ß£¬ŌŚBCĶ¬²ą×÷µČ±ßČż½ĒŠĪABDŗĶµČ±ßČż½ĒŠĪACE£¬Į¬½ÓCD£¬BE£®
ĶعżÖ¤Ć÷”÷””ADC”””Õ”÷””ABE””£¬µĆµ½DC=BE£»
£Ø2£©ČēĶ¼2£¬ĖıߊĪABCDÖŠ£¬µćE£¬F£¬G£¬H·Ö±šĪŖ±ßAB£¬BC£¬CD£¬DAµÄÖŠµć£¬Ė³“ĪĮ¬½ÓE”¢F”¢G”¢H£¬µĆµ½ĖıߊĪEFGH£¬ĪŅĆĒ³ĘĖıߊĪEFGHĪŖĖıߊĪABCDµÄÖŠµćĖıߊĪ£¬Į¬½ÓBD£¬ĄūÓĆČż½ĒŠĪÖŠĪ»ĻߵĊŌÖŹ£¬æɵĆEH”ĪBD£¬EH= ![]() BD£¬Ķ¬ĄķæɵĆFG”ĪBD£¬FG=
BD£¬Ķ¬ĄķæɵĆFG”ĪBD£¬FG= ![]() BD£¬ĖłŅŌEH”ĪFG£¬EH=FG£¬ĖłŅŌĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
BD£¬ĖłŅŌEH”ĪFG£¬EH=FG£¬ĖłŅŌĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»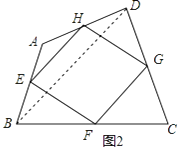
ĶŲÕ¹Ó¦ÓĆ
¢ŁČēĶ¼3£¬µćPŹĒĖıߊĪABCDÄŚŅ»µć£¬ĒŅĀś×ćPA=PB£¬PC=PD£¬”ĻAPB=”ĻCPD£¬µćE£¬F£¬G£¬H·Ö±šĪŖ±ßAB£¬BC£¬CD£¬DAµÄÖŠµć£¬²ĀĻėĖıߊĪEFGHµÄŠĪד£¬²¢Ö¤Ć÷£»
£Ø3£©Čōøıä£Ø2£©ÖŠµÄĢõ¼ž£¬Ź¹”ĻAPB=”ĻCPD=90”ć£¬ĘäĖūĢõ¼ž²»±ä£¬ĖıߊĪEFGHµÄŠĪדŹĒ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćP£Ø2£¬£3£©¹ŲÓŚxÖį¶Ō³ĘµćµÄ×ų±źŹĒ £Ø £©
A. £Ø”Ŗ2£¬£3£© B. £Ø2£¬3£© C. £Ø£2£¬3£© D. £Ø£3£¬2£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com