【题目】如图，在△ABC中，点D在BC上，DE∥AC，DF∥AB，下列四个判断中不正确的是( )
A.四边形AEDF是平行四边形
B.若∠BAC＝90°，则四边形AEDF是矩形
C.若AD平分∠BAC，则四边形AEDF是矩形
D.若AD⊥BC且AB＝AC，则四边形AEDF是菱形
【答案】C
【解析】
A选项，∵在△ABC中，点D在BC上，DE∥AC，DF∥AB，
∴DE∥AF，DF∥AE，
∴四边形AEDF是平行四边形；即A正确；
B选项，∵四边形AEDF是平行四边形，∠BAC=90°，
∴四边形AEDF是矩形；即B正确；
C选项，因为添加条件“AD平分∠BAC”结合四边形AEDF是平行四边形只能证明四边形AEDF是菱形，而不能证明四边形AEDF是矩形；所以C错误；
D选项，因为由添加的条件“AB=AC，AD⊥BC”可证明AD平分∠BAC，从而可通过证∠EAD=∠CAD=∠EDA证得AE=DE，结合四边形AEDF是平行四边形即可得到四边形AEDF是菱形，所以D正确.
故选C.
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，AD 是 BC 边上的高，且∠ACB＝∠BAD，AE 平分∠CAD，交 BC于点 E，过点 E 作 EF∥AC，分别交 AB、AD 于点 F、G．则下列结论：①∠BAC＝90°；②∠AEF＝∠BEF； ③∠BAE＝∠BEA； ④∠B＝2∠AEF，其中正确的有（ ）
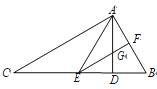
A. 4 个B. 3 个C. 2 个D. 1 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下面的解题过程，再解答问题：
如图①，已知AB∥CD，∠B＝40°，∠D＝30°，求∠BED的度数．
解：过点E作EF∥AB，则AB∥CD∥EF，
因为EF∥AB，所以∠1＝∠B＝40°
又因为CD∥EF，所以∠2＝∠D＝30°
所以∠BED＝∠1+∠2＝40°+30°＝70°．
如图②是小军设计的智力拼图玩具的一部分，现在小军遇到两个问题，请你帮他解决：
（1）如图②∠B＝45°，∠BED＝75°，为了保证AB∥CD，∠D必须是多少度？请写出理由．
（2）如图②，当∠G、∠GFP、∠P满足什么关系时，GH∥PQ，请直接写出满足关系的式子，并在如图②中画出需要添加的辅助线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知一次函数
与反比例函数
的图像相交于点
，与
轴相交于点
.
(1)填空:
的值为 ，
的值为 ；
(2)观察反比函数的图像，当
时，请直接写出自变量的取值范围；
(3)以
为边作菱形
，使点
在轴负半轴上，点
在第二象限内，求点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）在Rt△ABC中，∠BAC=
,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．
（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCFD 的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
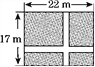
【题目】如图，在一块长为22 m，宽为17 m的矩形地面上，要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行)，剩余部分种上草坪，使草坪面积为300 m2.若设道路宽为x m，根据题意可列出方程为______________________________．
【答案】(22－x)(17－x)＝300(或x2－39x＋74＝0)
【解析】试题分析：把所修的两条道路分别平移到矩形的最上边和最左边，则剩下的草坪是一个长方形，根据长方形的面积公式列方程．设道路的宽应为x米，由题意有（22﹣x）（17﹣x）=300，故答案为：（22﹣x）（17﹣x）=300．
考点：由实际问题抽象出一元二次方程．
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根，则此方程的另一个根是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程：(1) 
； （2）
.
【答案】（1）x1 =1 ，x2=
； (2) x1 =-1，x2=
.
【解析】试题分析：
根据两方程的特点，使用“因式分解法”解两方程即可.
试题解析：
（1）原方程可化为： 
，
方程左边分解因式得： 
，
或
，
解得： 
， 
.
（2）原方程可化为： 
，即
，
∴
，
∴
或
，
解得： 
.
【题型】解答题
【结束】
20
【题目】已知x1，x2是关于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的两实根．
(1)若(x1－1)(x2－1)＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示8×7的正方形网格中，A（2，0），B（3，2），C（4，2），请按要求解答下列问题：
（1）将△ABO向右平移4个单位长度得到△A1B1O1，请画出△A1B1O1并写出点A1的坐标；
（2）将△ABO绕点C（4，2）顺时针旋转90°得到△A2B2O2，请画出△A2B2O2并写出点A2的坐标；
（3）将△A1B1O1绕点Q旋转90°可以和△A2B2O2完全重合，请直接写出点Q的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
