
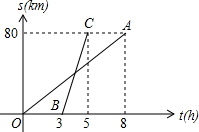
 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:分析 (1)用总路程除以各自用的时间即是各自的速度;
(2)设自行车出发后x小时,它们相遇,根据等量关系“自行车x小时走的路程=摩托车用(x-3)小时走的路程”列方程解答即可;
(3)分三种情形讨论即可;
解答 解:(1)摩托车每小时走:80÷(5-3)=40(千米),
自行车每小时走:80÷8=10(千米).
故答案为:40,10;
(2)设自行车出发后x小时,它们相遇,
10x=40(x-3)
解得x=4.
(3)设摩托车出发后t小时,他们相距10千米;
①相遇前:10(t+3)-40t=10,
解得t=$\frac{2}{3}$;
②相遇后:40t-10(t+3)=10,
解得:t=$\frac{4}{3}$,
③摩托车到达终点10(t+3)=70,解得t=4
答:摩托车出发后$\frac{2}{3}或\frac{4}{3}$或4小时,他们相距10千米.
点评 本题考查了函数的图象,学会看函数图象,从函数图象中获取信息,并且解决有关问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
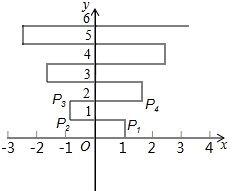 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )| A. | (26,50) | B. | (-26,50) | C. | (25,50) | D. | (-25,50) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC.
如图,△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
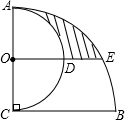 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π-4$ | C. | $3π-2\sqrt{3}$ | D. | 3π-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com