
【题目】解方程
(1)x2﹣6x﹣18=0(配方法)
(2)3(x﹣2)2=x(x﹣2)
(3)x2+2x﹣5=0
(4)(2x﹣3)2﹣2(2x﹣3)﹣3=0.
【答案】
(1)解:x2﹣6x﹣18=(x﹣3)2﹣27=0,
∴(x﹣3)2=27,x﹣3=±3 ![]() ,
,
∴x1=3 ![]() +3,x2=﹣3
+3,x2=﹣3 ![]() +3
+3
(2)解:原方程整理为:x2﹣5x+6=(x﹣2)(x﹣3)=0,
解得:x1=3,x2=2
(3)解:x2+2x﹣5=(x+1)2﹣6=0,
∴(x+1)2=6,x+1=± ![]() ,
,
∴x1= ![]() ﹣1,x2=﹣
﹣1,x2=﹣ ![]() ﹣1
﹣1
(4)解:设2x﹣3=y,则原方程变形为y2﹣2y﹣3=(y+1)(y﹣3)=0,
解得:y1=﹣1,y2=3.
当y=﹣1时,2x﹣3=﹣1,
解得:x=1;
当y=3时,2x﹣3=3,
解得:x=3.
∴方程(2x﹣3)2﹣2(2x﹣3)﹣3=0的解为3或1
【解析】(1)利用配方法可得出(x﹣3)2﹣27=0,解之即可得出结论;(2)将原方程进行整理后可得出x2﹣5x+6=0,利用分解因式法解方程即可得出结论;(3)利用配方法可得出(x+1)2﹣6=0,解之即可得出结论;(4)设2x﹣3=y,则原方程变形为y2﹣2y﹣3=0,利用分解因式法解方程即可求出y的值,再将其代入2x﹣3=y即可求出x的值,此题得解.
【考点精析】利用配方法和因式分解法对题目进行判断即可得到答案,需要熟知左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.


科目:初中数学 来源: 题型:
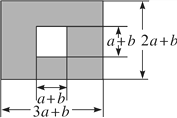
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,中间将修建一座边长为(a+b)米的正方形雕像,规划部门计划将余下部分进行绿化.
(1)试用含a,b的式子表示绿化部分的面积(结果要化简);
(2)若a=3,b=2,请求出绿化部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
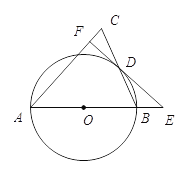
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
(1)求证:EF⊥AC;
(2)若AF=9,EF=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天的运营全是在东西走向的人民大街进行的,如果规定向东为正,向西为负,他这天下午的行车里程如下(单位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少?
(2)若汽车的耗油量为0.5L/㎞,那么这天下午汽车共耗油多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
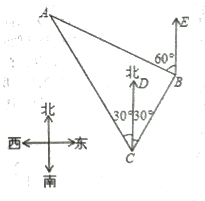
【题目】如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30。的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离姓B.(结果保留小数点后一位,其中![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衣,每件进价250元,开始以每件400元的价格销售,每星期能卖出20件,后来因库存积压,决定降价销售,经过两次降价后每件售价为324元,求每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知直线AC的函数解析式为y= ![]() x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位? 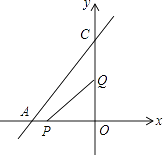
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com