Question

【题目】已知∠MAN．
（1）用尺规完成下列作图：（保留作图痕迹，不写作法）

①作∠MAN的平分线AE；
②在AE上任取一点F，作AF的垂直平分线分别与AM、AN交于P、Q；
（2）在（1）的条件下，线段AP与AQ有什么数量关系，请直接写出结论．

Answer 1

【答案】
（1）解：如图所示：

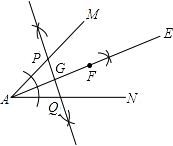
①AE为所求作的角平分线；

②PQ为所求作的垂直平分线

（2）解：AP=AQ．

证明：∵PQ是AB的垂直平分线，

∴∠PGA=∠QGA=90°，

∵AE是∠MAN的平分线，

∴∠PAG=∠QAG，

在△PAG和△QAG中，

，

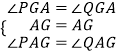∴△PAG≌△QAG（ASA），

∴AP=AQ

【解析】（1）①利用角平分线的作法得出即可；②利用垂直平分线的作法得出即可；（2）利用垂直平分线的性质得出∠PGA=∠QGA，进而得出△PAG≌△QAG（ASA），则AP=AQ，即可得出答案．
【考点精析】关于本题考查的线段垂直平分线的性质，需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案．