
 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.分析 (1)根据圆周角定理,由$\widehat{BD}$=$\widehat{AD}$得到∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE;
(2)连结OD,如图,利用内错角相等证明OD∥BC,而DE⊥BC,则OD⊥DE,于是根据切线的判定定理可得DE为⊙O的切线;
(3)作OH⊥BC于H,易得四边形ODEH为矩形,所以OD=EH=2,则CH=HE-CE=1,于是有∠HOC=30°,得到∠COD=60°,然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S扇形OCD-S△OCD进行计算.
解答 (1)证明:∵$\widehat{BD}$=$\widehat{AD}$,
∴∠BAD=∠ACD,
∵∠DCE=∠BAD,
∴∠ACD=∠DCE,
即CD平分∠ACE;
(2)解:直线ED与⊙O相切.理由如下:
连结OD,如图,
∵OC=OD,
∴∠OCD=∠ODC,
而∠OCD=∠DCE,
∴∠DCE=∠ODC,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴DE为⊙O的切线;
(3)解:作OH⊥BC于H,则四边形ODEH为矩形,
∴OD=EH,
∵CE=1,AC=4,
∴OC=OD=2,
∴CH=HE-CE=2-1=1,
在Rt△OHC中,∠HOC=30°,
∴∠COD=60°,
∴阴影部分的面积=S扇形OCD-S△OCD
=$\frac{60•π•{2}^{2}}{360}$-$\frac{\sqrt{3}}{4}$•22
=$\frac{2}{3}$π-$\sqrt{3}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形的计算.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | x>-1且x≠2 | B. | x≥-1 | C. | x≠-1 | D. | x>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:
某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
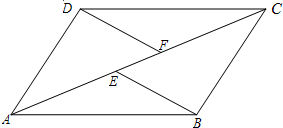 如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+a2=a4 | B. | (a3)3=a9 | C. | (a+1)2=a2+1 | D. | 1+$\frac{1}{a}=\frac{2}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
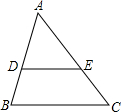 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{3}{2}$,则$\frac{EC}{AE}$=$\frac{2}{3}$.
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{3}{2}$,则$\frac{EC}{AE}$=$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com