
 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.分析 (1)利用三角形三边的关系得到3<2x-1<9,然后解不等式组,再确定不等式组的整数解即可;
(2)先作线段AB=3,再以A、B为圆心,6和5为半径画弧交于点C,则△ABC满足条件;作BH⊥AC于H,如图,则利用勾股定理可计算出BH,从而得到三角形面积,然后根据三角形的内切圆半径与三角形的周长积的一半等于三角形面积求三角形的内切圆半径.
解答 解:(1)由题得:3<2x-1<9,
而2x-1为整数,
∴2x-1的值为4、5、6、7、8,
∴符合条件的三角形为(3,6,5)、(3,6,4),(3,6,7),(3,6,6),(3,6,8);
(2)由(1)得:作边长为3,6,5的三角形,
如图,△ABC为所作,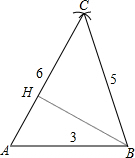
作BH⊥AC于H,如图,设三角形的内切圆半径为r,AH=x,则CH=6-x,
在Rt△ABH,BH2=AB2-AH2=32-x2,
在Rt△CBH,BH2=CB2-CH2=52-(6-x)2,
∴32-x2=52-(6-x)2,解得x=$\frac{5}{3}$,
∴BH=$\sqrt{{3}^{2}-(\frac{5}{3})^{2}}$=$\frac{2\sqrt{14}}{3}$,
∵$\frac{1}{2}$r(AB+BC+AC)=$\frac{1}{2}$•BH•AC,
∴r=$\frac{4\sqrt{14}}{14}$=$\frac{2\sqrt{14}}{7}$,
此三角形内切圆半径为$\frac{2\sqrt{14}}{7}$.
当三角形三边为3,6,4时,同法可得内切圆半径为$\frac{\sqrt{455}}{26}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.计算三角形的内切圆半径的关键是运用三角形的内切圆半径与三角形的周长积的一半等于三角形面积.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:填空题
 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2
已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
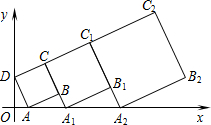 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 队员1 | 队员2 | 队员3 | 队员4 | |
| 甲组 | 176 | 177 | 175 | 176 |
| 乙组 | 178 | 175 | 177 | 174 |
| A. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2<S乙2 | B. | $\overline{{x}_{甲}}=\overline{{x}_{乙}}$,S甲2>S乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,S甲2<S乙2 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,S甲2>S乙2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 科目 | 篮球 | 围棋 | 剪纸 | 舞台剧 | 茶艺 | 交谊舞 | 其它课 |
| 计数 | 正正 |  | 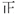 | 正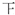 | 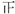 | 正一 | 正一 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
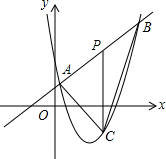 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com