
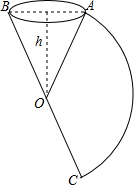
 如图,将扇形AOC围成一个圆锥的侧面.已知围成的圆锥的高为12,扇形AOC的弧长为10π,则圆锥的侧面积为65π.
如图,将扇形AOC围成一个圆锥的侧面.已知围成的圆锥的高为12,扇形AOC的弧长为10π,则圆锥的侧面积为65π.  仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):
某化妆公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售费中提取一定数量的费用):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
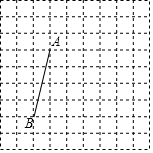 如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+a3=a5 | B. | (a3)2÷a6=1 | C. | a2•a3=a6 | D. | ($\sqrt{2}$+$\sqrt{3}$)2=5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com