
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.

(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答下列问题:
小明遇到这样一个问题,如图,在![]() 中,
中,![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.
小明发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图)
,经过推理和计算能够使问题得到解决(如图)

请你回答:
(1)证明:![]() ;
;
(2)求出![]() 的值;
的值;
(3)参考小明思考问题的方法,解决问题;
如图,已知![]() 和矩形
和矩形![]() 与
与![]() 交于点
交于点![]() .求
.求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.

(1)直接写出当点C运动到线段OB的中点时,求t的值及点E的坐标.
(2)当点C在线段OB上运动时,四边形ADEC的面积为S.
①求证:四边形ADEC为平行四边形.
②写出s与t的函数关系式,并求出t的取值范围.
(3)是否存在某一时刻,使OC是PC的一半?若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在普通商场中用96元购买了一种商品,后来他在网上发现完全相同的这一商品在网上购买比普通商场中每件少2元,他用90元在网上再次购买这一商品,比上次在普通商场中多买了3件.问小明在网上购买的这一商品每件几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A表示的数为9,动点B,C在数轴上移动,且总保持BC=2(点C在点B右侧),设点B表示的数为m.
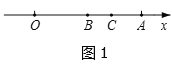

(1) 如图1,当B,C在线段OA上移动时,
① 若B为OA中点,则AC= ;
② 若B,C移动到某一位置时,恰好满足AC=OB,求此时m的值;
(2) 当线段BC沿射线AO方向移动时,若存在AC-OB=![]() AB,求满足条件的m值.
AB,求满足条件的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
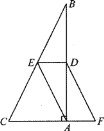
【题目】如图,Rt△ABC,∠BAC=90°,点D,E分别为边AB,BC的中点,点F在CA延长线上,且∠FDA=∠B.
(1)求证:AF=DE;
(2)若AC=3,BC=5,求四边形AEDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
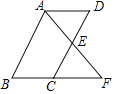
【题目】如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若AB=8,BC=5,则EF的长为 时,AB⊥AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com