
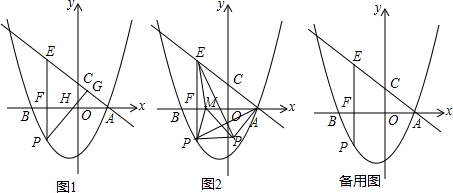
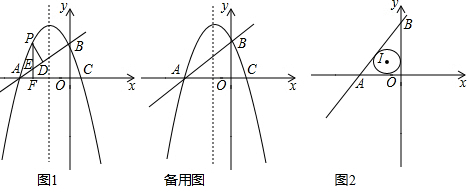
分析 (1)先令y=0求抛物线与x轴交点坐标,利用待定系数法求直线AC的解析式;
(2)如图1中,设点P(m,$\frac{1}{2}$m2+$\frac{1}{2}$m-3),则E(m,-$\frac{3}{4}$m+$\frac{3}{2}$),构建关于x的二次函数,利用二次函数的性质即可解决问题.
(3)如图2中,分四种情形讨论即可①当P1P=P1A时,②AP=AP2时,③当P3P=P3A时,④当P4P=PA时,画出图形,求出点M坐标即可.
解答 解:(1)当y=0时,$\frac{1}{2}$x2+$\frac{1}{2}$x-3=0,解得x1=-3,x2=2,
∵点A在点B的右侧,
∴A(2,0)、B(-3,0);
设直线AC的解析式为y=kx+b,
把A(2,0)、C(0,$\frac{3}{2}$)代入得:$\left\{\begin{array}{l}{2k+b=0}\\{b=\frac{3}{2}}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线AC的解析式为:y=-$\frac{3}{4}x+\frac{3}{2}$;
(2)如图1中,在Rt△ACO中,tan∠OAC=$\frac{CO}{AO}$=$\frac{3}{4}$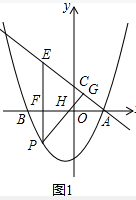
∵∠FPH+∠PHF=90°,∠OAC+∠AHG=90°,∠PHF=∠AHG,
∴∠HPF=∠OAC
∴tan∠FPH=tan∠OAC=$\frac{3}{4}$
∵tan∠FPH=$\frac{FH}{FP}$
∴$\frac{2}{3}$FH=$\frac{2}{3}$×FP×$\frac{3}{4}$=$\frac{1}{2}$FP
设点P(m,$\frac{1}{2}$m2+$\frac{1}{2}$m-3),则E(m,-$\frac{3}{4}$m+$\frac{3}{2}$),
∴EP=-$\frac{1}{2}$m2-$\frac{5}{4}$m+$\frac{9}{2}$,FP=-$\frac{1}{2}$m2-$\frac{1}{2}$m+3,
于是l=EP-$\frac{2}{3}$FH=EP-$\frac{1}{2}$FP=-$\frac{1}{4}$m2-m+3,
∵-$\frac{1}{4}$<0
∴l=-$\frac{1}{4}$m2-m+3开口向下,对称轴x=$\frac{-1}{-2×(-\frac{1}{4})}$=-2,
∵点P是x轴下方的抛物线上一动点,
∴-3<m<2
∴l在-3<m<2时,当m=-2时,l最大=4;
(3)如图2中,m=-2时,E(-2,3),P(-2,-2),
∵A(2,0),
∴EP=EA=5,
①当P1P=P1A时,AP中点K(0,-1),于是直线EK为y=-2x-1,
∴直线EK交x于I(-$\frac{1}{2}$,0),EI=$\frac{3}{2}$$\sqrt{5}$,
过点M1作M1J⊥EK于J,则EJ=EF=3,
∴IJ=$\frac{3}{2}$$\sqrt{5}$-3,
∵△IEF∽△IM1J,
∴$\frac{IE}{I{M}_{1}}$=$\frac{IF}{IJ}$,
∴IM1=$\frac{15}{2}$-3$\sqrt{5}$.
∴M1(3$\sqrt{5}$-8,0),
②AP=AP2时,△AEP≌△AEP2,
∴∠AEP=∠AEP2,
∴点M2与点A重合,
∴点M2(2,0).
③当P3P=P3A时,由△EFM3∽△M1FE,得到EF2=FM3•FM1,
∴FM3=3$\sqrt{5}$+6,
∴点M3(-3$\sqrt{5}$-8,0),
④当P4P=PA时,作M4Q⊥EP4,设M4Q=M4F=x,
在RT△P4QM4中,
∵P4Q2+QM42=FP42,
∴22+x2=(4-x)2,
∴x=$\frac{3}{2}$,
∴0M4=$\frac{3}{2}$+2=$\frac{7}{2}$,
∴点M4(-$\frac{7}{2}$,0).
综上所述点M1(3$\sqrt{5}$-8,0),M2(2,0),M3(-3$\sqrt{5}$-8,0),M4(-$\frac{7}{2}$,0).
点评 本题考查二次函数综合题、待定系数法、函数最值问题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会构建二次函数,解决实际问题中最值问题,学会分类讨论,考虑问题要全面,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
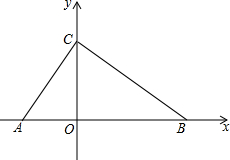 如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.
如图,在平面直角坐标系中,点A,B,C在坐标轴上,∠ACB=90°,OC,OB的长分别是方程x2-7x+12=0的两个根,且OC<OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com