
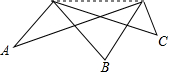
 如图,三名足球运动员在不同的位置射门,你觉得哪个位置射门进球的可能性最大?哪个位置射门进球的可能性最小?你是怎么想的?与同伴交流.
如图,三名足球运动员在不同的位置射门,你觉得哪个位置射门进球的可能性最大?哪个位置射门进球的可能性最小?你是怎么想的?与同伴交流. 分析 作△MNC的外接圆⊙O,交AN于点E,延长MB交⊙O于点F,连接NF,根据圆周角定理可得∠C=∠F=∠MEN,由∠MBN>∠F即∠MBN>∠C、∠MEN>∠,即∠C>∠A可得∠MBN>∠C>∠A,即可作出判断.
解答 解:在点B位置射门进球的可能性最大,在点A位置射门进球的可能性最小,
如图,作△MNC的外接圆⊙O,交AN于点E,延长MB交⊙O于点F,连接NF,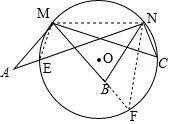
则∠C=∠F=∠MEN,
∵∠MBN>∠F,即∠MBN>∠C,
∠MEN>∠A,即∠C>∠A,
∴∠MBN>∠C>∠A,
∴在点B位置射门进球的可能性最大,在点A位置射门进球的可能性最小.
点评 本题主要考查可能性的大小和圆周角定理,了解射门角度越大进球的可能性越大是解题的前提,熟练掌握圆周角定理是解题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
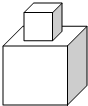 如图所示的某种玩具是由两个正方体用胶水粘合而成的,它们的棱长分别为1米和3 米,为了美观,现要在其表面喷涂油漆,已知喷涂1平方米需用油漆30克,那么喷涂这个玩具共需油漆1740克.
如图所示的某种玩具是由两个正方体用胶水粘合而成的,它们的棱长分别为1米和3 米,为了美观,现要在其表面喷涂油漆,已知喷涂1平方米需用油漆30克,那么喷涂这个玩具共需油漆1740克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
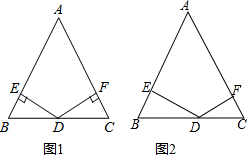 (1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB于点E、DF⊥AC于点F.求证:DE=DF;
(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB于点E、DF⊥AC于点F.求证:DE=DF;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
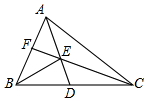 如图,△ABC中,E为AD与CF的交点,AE=ED,已知三角形ABC面积是1,三角形BEF的面积是$\frac{1}{10}$.求:
如图,△ABC中,E为AD与CF的交点,AE=ED,已知三角形ABC面积是1,三角形BEF的面积是$\frac{1}{10}$.求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2,-1,0,1,2,3 | B. | -2,-1,0,1,2 | C. | -2,-1,0,1,2,3 | D. | -1,0,1,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
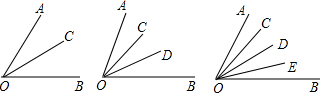
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com