
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:∵3.1415是有限小数,
∴3.1415是有理数;
∵$\sqrt{9}=3$,3是整数,
∴$\sqrt{9}$是有理数;
∵$\frac{1}{7}=0.\stackrel{•}{1}4285\stackrel{•}{7}$,$0.\stackrel{•}{1}4285\stackrel{•}{7}$是循环小数,
∴$\frac{1}{7}是有理数$;
∵$\sqrt{5}=2.236…$,π=3.14159…,$\sqrt{8}=2\sqrt{2}=2.828…$,2.1010010001…都是无限不循环小数,
∴$\sqrt{5}、π、\sqrt{8}$、2.1010010001…都是无理数,一共有4个.
故选:C.
点评 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
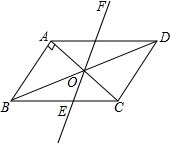 如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | x2-2=(x+3)2 | C. | 2x+3x-5=0 | D. | x2-1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | $\sqrt{32}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
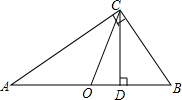 如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.
如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com