
分析 设冠军选手的平均速度是xkm/h,陈老师的平均速度是$\frac{1}{3}$xkm/h,根据$\frac{路程}{速度}$=时间列出方程,求出x的值,即可得出答案.
解答 解:设冠军选手的平均速度是xkm/h,陈老师的平均速度是$\frac{1}{3}$xkm/h,根据题意得:
$\frac{7.5}{\frac{1}{3}x}$-$\frac{15}{x}$=$\frac{1}{4}$,
解得:x=30,
经检验x=30是原方程的解,
则30×$\frac{1}{3}$=10km/h,
答:冠军选手的平均速度是30km/h,陈老师的平均速度是10km/h.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系,列出方程是解决问题的关键;用到的知识点是:$\frac{路程}{速度}$=时间.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.
星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
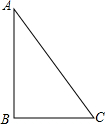 如图,Rt△ABC中,∠B=90°,AB=3,AC=5.
如图,Rt△ABC中,∠B=90°,AB=3,AC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)
如图所示,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2,试判断∠AGD和∠ACB是否相等,为什么?(将解答过程补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=x+1与$y=-\frac{3}{4}x+3$交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
如图,在平面直角坐标系中,直线y=x+1与$y=-\frac{3}{4}x+3$交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com