
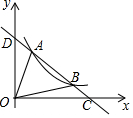
 ��ͼ����D�ǡ�ABC�ı�AB�ϵ�һ�㣬DE��BC��AC�ڵ�E����DF��AC��BC�ڵ�F���ֱ�ǡ�ADE����BDF��?DFCE����ABC�����ΪS1��S2��S3��S�����½��ۣ�
��ͼ����D�ǡ�ABC�ı�AB�ϵ�һ�㣬DE��BC��AC�ڵ�E����DF��AC��BC�ڵ�F���ֱ�ǡ�ADE����BDF��?DFCE����ABC�����ΪS1��S2��S3��S�����½��ۣ����� �ٸ������������ε�����ȵ������Ʊȵ�ƽ���ó�AD=BD�����AE=CE�����ɵó��𰸣�
�ڸ������������ε�����ȵ������Ʊȵ�ƽ���ó�AM=2MN�����ɵó��𰸣�
����ƽ���߿ɵö�Ӧ�߶γɱ������������������ε�����ȵ��ڶ�Ӧ�ߵ�ƽ���ȣ�����������⼴�ɣ�
�ܽ����ֻ�軭��ʾ��ͼ�����жϳ���BFD�ס�DEA��Ȼ���������ȵ������Ʊȵ�ƽ���ó���ABC���������������SDECF=SABC-SADE-SDBF�ɵó���
��� �⣺�١���DE��BC��DF��AC��
���ADE�ס�ABC����BDF�ס�BAC��
��S1=S2��
�ࣨ$\frac{AD}{AB}$��2=��$\frac{BD}{AB}$��2��
��AD=BD��
��DE��BC��
��AE=EC��
��DE�ǡ�ABC����λ�ߣ������ȷ��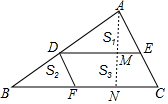
�ڡ���A��AN��BC��N����DE��M��
��DE��BC��
��AN��DE��
��DE��BC��DF��AC��
���ı���DECF��ƽ���ı��Σ�
��DE=CF��
��S1=S3��
��$\frac{1}{2}��DE��AM$=CF��MN��
��AM=2MN��
��DE��BC��
���ADE��ABC��
��$\frac{DE}{BC}$=$\frac{AM}{AN}$=$\frac{2MN}{2MN+MN}$=$\frac{2}{3}$��
��2BC=3DE�������ȷ��
�ۡ���DE��BC��DF��AC
���ı���DECF��ƽ���ı��Σ�
��DE=CF��DF=CE��
�����������ε�����ȵ��ڶ�Ӧ�ߵ�ƽ���ȣ�
��$\frac{\sqrt{{S}_{1}}}{\sqrt{S}}$=$\frac{AD}{AB}$��$\frac{\sqrt{{S}_{2}}}{\sqrt{S}}$=$\frac{BD}{AB}$��
��$\frac{\sqrt{{S}_{1}}}{\sqrt{S}}$+$\frac{\sqrt{{S}_{2}}}{\sqrt{S}}$=$\frac{AD}{AB}$+$\frac{BD}{AB}$=1��
��$\sqrt{S}$=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$����۴���
�ܡ�������ã���BFD�ס�DEA��
��ɵã�$\frac{BD}{AD}$=$\sqrt{\frac{{S}_{2}}{{S}_{1}}}$������ȵ������Ʊȵ�ƽ������
��$\frac{BD}{AB}$=$\frac{\sqrt{\frac{{S}_{2}}{{S}_{1}}}}{1+\sqrt{\frac{{S}_{2}}{{S}_{1}}}}$����$\sqrt{\frac{{S}_{2}}{{S}_{1}}}$=x��
��SABC=S��
��$\frac{{S}_{2}}{S}$=��$\frac{BD}{AB}$��2��
��ɵ�S=S1+S2+2S1$\sqrt{\frac{{S}_{2}}{{S}_{1}}}$��
�֡ߡ�ADE����DBF������ֱ�ΪS1��S2��
��SDECF=SABC-SADE-SDBF=2S1$\sqrt{\frac{{S}_{2}}{{S}_{1}}}$=2$\sqrt{{S}_{1}•{S}_{2}}$�������ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� ���⿼����������Ȼ��任�����������ε����ʺ��ж��ȣ��Ѷ����У����ڴ�����ĿҪ�ȸ������Ƶó�����ʽ��Ȼ����ݱ��������ʵó�Ҫ��ͼ�ε��������ʽ�������ó��𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬ֱ�DZ���������DEFG�ı߳���Ϊ2����AC��DE��ͬһֱ���ϣ���ʼʱ��C���D�غϣ��á�ABC������ֱ������ƽ�ƣ�ֱ����A���E�غ�Ϊֹ����CD�ij�Ϊx����ABC��������DEFG�غϲ��֣�ͼ����Ӱ���֣������Ϊy����y��x֮��ĺ�����ϵ��ͼ������ǣ�������
��ͼ��ʾ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬ֱ�DZ���������DEFG�ı߳���Ϊ2����AC��DE��ͬһֱ���ϣ���ʼʱ��C���D�غϣ��á�ABC������ֱ������ƽ�ƣ�ֱ����A���E�غ�Ϊֹ����CD�ij�Ϊx����ABC��������DEFG�غϲ��֣�ͼ����Ӱ���֣������Ϊy����y��x֮��ĺ�����ϵ��ͼ������ǣ�������| A�� |  | B�� | 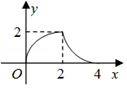 | C�� | 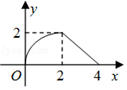 | D�� | 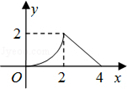 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{6}{x}$��x��0����ͼ����A��m��6����B��3��n�����㣬��x�ύ�ڵ�C����y�ύ�ڵ�D�����н��ۣ���һ�κ�������ʽΪy=-2x+8����AD=BC����kx+b-$\frac{6}{x}$��0�Ľ⼯Ϊ0��x��1��x��3���ܡ�AOB�������8��������ȷ���۵ĸ����ǣ�������
��ͼ��һ�κ���y=kx+b�뷴��������y=$\frac{6}{x}$��x��0����ͼ����A��m��6����B��3��n�����㣬��x�ύ�ڵ�C����y�ύ�ڵ�D�����н��ۣ���һ�κ�������ʽΪy=-2x+8����AD=BC����kx+b-$\frac{6}{x}$��0�Ľ⼯Ϊ0��x��1��x��3���ܡ�AOB�������8��������ȷ���۵ĸ����ǣ�������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=a4 | B�� | a2•a3=a6 | C�� | a2��a-2=a4 | D�� | ��a2��3=a8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�κ���y1=k1x+b��ͼ���뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ���ཻ��A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����B�������ǣ�m��-4��������AO��AO=5��sin��AOC=$\frac{3}{5}$��
��ͼ��һ�κ���y1=k1x+b��ͼ���뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ���ཻ��A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����B�������ǣ�m��-4��������AO��AO=5��sin��AOC=$\frac{3}{5}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com