
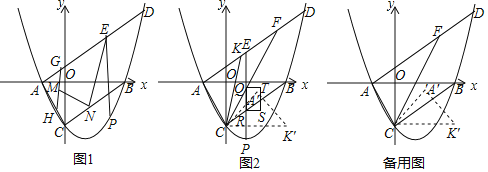
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=![]() ÓėxÖį½»ÓŚA£¬B£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬Į¬½ÓAC”¢BC£®¹żµćA×÷AD”ĪBC½»Å×ĪļĻßÓŚµćD£Ø8
ÓėxÖį½»ÓŚA£¬B£ØµćAŌŚµćBµÄ×ó²ą£©ÓėyÖį½»ÓŚµćC£¬Į¬½ÓAC”¢BC£®¹żµćA×÷AD”ĪBC½»Å×ĪļĻßÓŚµćD£Ø8![]() £¬10£©£¬µćPĪŖĻ߶ĪBCĻĀ·½Å×ĪļĻßÉĻµÄČĪŅāŅ»µć£¬¹żµćP×÷PE”ĪyÖį½»Ļ߶ĪADÓŚµćE£®
£¬10£©£¬µćPĪŖĻ߶ĪBCĻĀ·½Å×ĪļĻßÉĻµÄČĪŅāŅ»µć£¬¹żµćP×÷PE”ĪyÖį½»Ļ߶ĪADÓŚµćE£®
£Ø1£©ČēĶ¼1£®µ±PE+AE×ī“óŹ±£¬·Ö±šČ”Ļ߶ĪAE£¬ACÉĻ¶ÆµćG£¬H£¬Ź¹GH=5£¬ČōµćMĪŖGHµÄÖŠµć£¬µćNĪŖĻ߶ĪCBÉĻŅ»¶Æµć£¬Į¬½ÓEN”¢MN£¬ĒóEN+MNµÄ×īŠ”Öµ£»
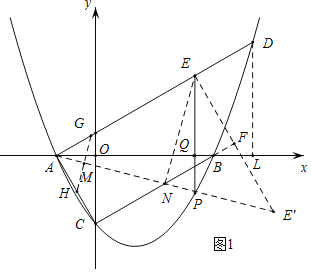
£Ø2£©ČēĶ¼2£¬µćFŌŚĻ߶ĪADÉĻ£¬ĒŅAF£ŗDF=7£ŗ3£¬Į¬½ÓCF£¬µćQ£¬R·Ö±šŹĒPEÓėĻ߶ĪCF£¬BCµÄ½»µć£¬ŅŌRQĪŖ±ß£¬ŌŚRQµÄÓŅ²ą×÷¾ŲŠĪRQTS£¬ĘäÖŠRS=2£¬×÷”ĻACBµÄ½ĒĘ½·ÖĻßCK½»ADÓŚµćK£¬½«”÷ACKČʵćCĖ³Ź±ÕėŠż×Ŗ75”ćµĆµ½”÷A”äCK”䣬µ±¾ŲŠĪRQTSÓė”÷A”äCK”äÖŲµž²æ·Ö£ØĆ껿²»ĪŖ0£©ĪŖÖį¶Ō³ĘĶ¼ŠĪŹ±£¬ĒėÖ±½ÓŠ“³öµćPŗį×ų±źµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©2![]() -
-![]() £Ø2£©µ±xP=2
£Ø2£©µ±xP=2![]() -1»ņ2
-1»ņ2![]() £¼xP£¼6
£¼xP£¼6![]() -6
-6![]() Ź±£¬¾ŲŠĪRQRSŗĶ”÷A”äCK”äÖŲµž²æ·ÖĪŖÖį¶Ō³ĘĶ¼ŠĪ
Ź±£¬¾ŲŠĪRQRSŗĶ”÷A”äCK”äÖŲµž²æ·ÖĪŖÖį¶Ō³ĘĶ¼ŠĪ
”¾½āĪö”æ
£Ø1£©ĻČĶعż¶ž“ĪŗÆŹż½āĪöŹ½Ēó³öµćA£¬BµÄ×ų±ź£¬ŌŁĒó³öAC£¬AB£¬CBµÄ³¤¶Č£¬ÓĆ¹“¹É¶ØĄķÄę¶ØĄķÖ¤Ö±½ĒČż½ĒŠĪ£¬Ēó³öÖ±ĻßADµÄ½āĪöŹ½£¬ÓĆŗ¬ĻąĶ¬×ÖÄøµÄ“śŹżŹ½·Ö±š±ķŹ¾E£¬Q£¬PµÄ×ų±ź£¬²¢±ķŹ¾³öEP³¤¶Č£¬Ēó³öAE³¤¶Č£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹĒó³öEA+EP×ī“óÖµŹ±µćEµÄ×ų±ź£®×īŗó×÷³öµćE¹ŲÓŚCBµÄ¶Ō³Ęµć£¬ĄūÓĆĮ½µćÖ®¼äĻ߶Ī×ī¶ĢæÉĒó³ö½į¹ū£»
£Ø2£©ÓÉŠż×ŖµÄŠŌÖŹµĆµ½Čż½ĒŠĪCA”äKÓėČż½ĒŠĪCAKČ«µČ£¬ĒŅĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Ēó³öA”䣬K”äµÄ×ų±ź£¬Ēó³öÖ±ĻßA”äK”ä¼°CBµÄ½āĪöŹ½£¬Ēó³ö½»µć×ų±ź£¬ĶعżĶ¼Ļó¹Ū²ģ³öPµÄŗį×ų±źµÄȔֵ·¶Ī§£®
£Ø1£©ŌŚÅ×ĪļĻßy=![]() x2-
x2-![]() x-6ÖŠ£¬
x-6ÖŠ£¬
µ±y=0Ź±£¬x1=-2![]() £¬x2=6
£¬x2=6![]() £¬
£¬
µ±x=0Ź±£¬y=-6£¬
”ßÅ×ĪļĻßy=![]() x2-
x2-![]() x-6ÓėxÖį½»ÓŚA£¬B£ØµćAŌŚµćB×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬
x-6ÓėxÖį½»ÓŚA£¬B£ØµćAŌŚµćB×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬
”ąA£Ø-2![]() £¬0£©£¬B£Ø6
£¬0£©£¬B£Ø6![]() £¬0£©£¬C£Ø0£¬-6£©£¬
£¬0£©£¬C£Ø0£¬-6£©£¬
”ąAB=8![]() £¬AC=
£¬AC=![]() £¬BC=
£¬BC=![]() £¬
£¬
ŌŚ”÷ABCÖŠ£¬
AC2+BC2=192£¬AB2=192£¬
”ąAC2+BC2=AB2£¬
”ą”÷ABCŹĒÖ±½ĒČż½ĒŠĪ£¬ĒŅ”ĻACB=90”ć£¬
”ßAD”ĪBC£¬
”ą”ĻCAD=90”ć£¬
¹żµćD×÷DL”ĶxÖįÓŚµćL£¬
ŌŚRt”÷ADLÖŠ£¬
DL=10£¬AL=10![]() £¬
£¬
tan”ĻDAL=![]() =
=![]() £¬
£¬
”ą”ĻDAB=30”ć£¬
°ŃµćA£Ø-2![]() £¬0£©£¬D£Ø8
£¬0£©£¬D£Ø8![]() £¬10£©“śČėÖ±Ļß½āĪöŹ½£¬
£¬10£©“śČėÖ±Ļß½āĪöŹ½£¬
µĆ![]() £¬
£¬
½āµĆk=![]() £¬b=2£¬
£¬b=2£¬
”ąyAD=![]() x+2£¬
x+2£¬
ÉčµćEµÄŗį×ų±źĪŖa£¬EP”ĶyÖįÓŚµćQ£¬
ŌņE£Øa£¬![]() a+2£©£¬Q£Øa£¬0£©£¬P£Øa£¬
a+2£©£¬Q£Øa£¬0£©£¬P£Øa£¬![]() a2-
a2-![]() a-6£©£¬
a-6£©£¬
”ąEQ=![]() a+2£¬EP=
a+2£¬EP=![]() a+2-£Ø
a+2-£Ø![]() a2-
a2-![]() a-6£©=
a-6£©=![]() a2+
a2+![]() a+8£¬
a+8£¬
”ąŌŚRt”÷AEBÖŠ£¬
AE=2EQ=![]() a+4£¬
a+4£¬
”ąPE+AE=![]() a+4+£Ø
a+4+£Ø![]() a2+
a2+![]() a+8£©
a+8£©
=![]() a2
a2![]() a+12
a+12
=![]() £Øa-5
£Øa-5![]() £©2+
£©2+![]()
”ąøł¾ŻŗÆŹżµÄŠŌÖŹæÉÖŖ£¬µ±a=5![]() Ź±£¬PE+AEÓŠ×ī“óÖµ£¬
Ź±£¬PE+AEÓŠ×ī“óÖµ£¬
”ą“ĖŹ±E£Ø5![]() £¬7£©£¬
£¬7£©£¬
¹żµćE×÷EF”ĶCB½»CBµÄŃÓ³¤ĻßÓŚµćF£¬
Ōņ”ĻEAC=”ĻACB=”ĻACF=90”ć£¬
”ąĖıߊĪACFEŹĒ¾ŲŠĪ£¬
×÷µćE¹ŲÓŚCBµÄ¶Ō³ĘµćE'£¬
ŌŚ¾ŲŠĪACFEÖŠ£¬ÓɾŲŠĪµÄŠŌÖŹ¼°Ę½ŅĘ¹ęĀÉÖŖ£¬
xF-xE=xC-xA£¬yE-yF=yA-yC£¬
”ßA£Ø-2![]() £¬0£©£¬C£Ø0£¬-6£©£¬E£Ø5
£¬0£©£¬C£Ø0£¬-6£©£¬E£Ø5![]() £¬7£©£¬
£¬7£©£¬
”ąxF-5![]() =0-£Ø-2
=0-£Ø-2![]() £©£¬7-yF=0-£Ø-6£©£¬
£©£¬7-yF=0-£Ø-6£©£¬
”ąxF=7![]() £¬yF=1£¬
£¬yF=1£¬
”ąF£Ø7![]() £¬1£©£¬
£¬1£©£¬
”ßFŹĒEE”äµÄÖŠµć£¬
”ą![]() £¬
£¬![]() £¬
£¬
”ąxE”ä=9![]() £¬yE”ä=-5£¬
£¬yE”ä=-5£¬
”ąE'£Ø9![]() £¬-5£©£¬
£¬-5£©£¬
Į¬½ÓAE'£¬½»BCÓŚµćN£¬Ōņµ±GHµÄÖŠµćMŌŚE”äAÉĻŹ±£¬EN+MNÓŠ×īŠ”Öµ£¬
”ąAE”ä=![]() =2
=2![]() £¬
£¬
”ßMŹĒRt”÷AGHŠ±±ßÖŠµć£¬
”ąAM=![]() GH=
GH=![]() £¬
£¬
”ąEN+MN=E”äM=2![]() -
-![]() £¬
£¬
”ąEN+MNµÄ×īŠ”ÖµŹĒ2![]() -
-![]() £®
£®
£Ø2£©ŌŚRt”÷AOCÖŠ£¬
”ßtan”ĻACO=![]() =
=![]() £¬
£¬
”ą”ĻAOC=30”ć£¬
”ßKEĘ½·Ö”ĻACB£¬
”ą”ĻACK=”ĻBCK=45”ć£¬
ÓÉŠż×ŖÖŖ£¬”÷CA”äK”ä”Õ”÷CAK£¬”ĻAC”äA”ä=75”ć£¬
”ą”ĻOCA”ä=75”ć-”ĻACO=45”ć£¬”ĻAC”äK”ä=45”ć£¬
”ąOCK”ä=90”ć£¬
”ąK”äC”ĶyÖį£¬”÷CAK”äŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąA”äC=AC=4![]() £¬
£¬
”ąxA”ä=![]() =2
=2![]() £¬yA”ä=2
£¬yA”ä=2![]() -6£¬
-6£¬
”ąA”ä£Ø2![]() £¬2
£¬2![]() -6£©£¬
-6£©£¬
”ąK”ä£Ø4![]() £¬-6£©£¬
£¬-6£©£¬
½«A”ä£Ø2![]() £¬2
£¬2![]() -6£©£¬K”ä£Ø4
-6£©£¬K”ä£Ø4![]() £¬-6£©£¬“śČėŅ»“ĪŗÆŹż½āĪöŹ½£¬
£¬-6£©£¬“śČėŅ»“ĪŗÆŹż½āĪöŹ½£¬
µĆ![]() £¬
£¬
½āµĆk=-1£¬b=4![]() -6£¬
-6£¬
”ąyA”äK”ä=-x+4![]() -6£¬
-6£¬
”ßCB”ĪAD£¬
”ą½«µćC£Ø0£¬-6£©£¬B£Ø6![]() £¬0£©“śČėŅ»“ĪŗÆŹż½āĪöŹ½£¬
£¬0£©“śČėŅ»“ĪŗÆŹż½āĪöŹ½£¬
µĆ![]() £¬
£¬
½āµĆk=![]() £¬b=-6£¬
£¬b=-6£¬
”ąyCB=![]() x-6£¬
x-6£¬
ĮŖĮ¢yA”äK”ä=-x+4![]() -6ŗĶyCB=
-6ŗĶyCB=![]() x-6£¬
x-6£¬
µĆ-x+4![]() -6=
-6=![]() x-6£¬
x-6£¬
”ąx=6![]() -6
-6![]() £¬
£¬
”ąÖ±ĻßCBÓėA”äK”äµÄ½»µćŗį×ų±źŹĒ6![]() -6
-6![]() £¬
£¬
”ßµ±EP¾¹żA”䏱£¬µćPµÄŗį×ų±źŹĒ2![]() £¬
£¬
”ąČēĶ¼2£¬µ±2![]() £¼xP£¼6
£¼xP£¼6![]() -6
-6![]() Ź±£¬ÖŲµž²æ·ÖŹĒÖį¶Ō³ĘĶ¼ŠĪ£»
Ź±£¬ÖŲµž²æ·ÖŹĒÖį¶Ō³ĘĶ¼ŠĪ£»

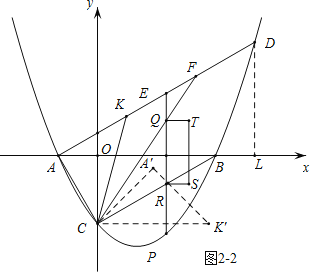
ČēĶ¼3£¬ÓÉÓŚRSµÄ³¤¶ČĪŖ2£¬ÓÉĶ¼æÉ擳öµ±xP=2![]() -1Ź±£¬ÖŲµž²æ·ÖĶ¬ŃłĪŖÖį¶Ō³ĘĶ¼ŠĪ£»
-1Ź±£¬ÖŲµž²æ·ÖĶ¬ŃłĪŖÖį¶Ō³ĘĶ¼ŠĪ£»
×ŪÉĻ£¬µ±xP=2![]() -1»ņ2
-1»ņ2![]() £¼xP£¼6
£¼xP£¼6![]() -6
-6![]() Ź±£¬
Ź±£¬
¾ŲŠĪRQRSŗĶ”÷A”äCK”äÖŲµž²æ·ÖĪŖÖį¶Ō³ĘĶ¼ŠĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
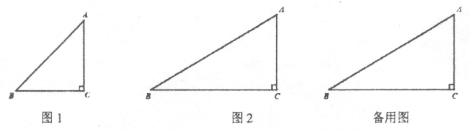
”¾ĢāÄæ”æŅŃÖŖRt”÷ABC£¬”ĻC=90”ć£¬CD”ĶABÓŚD.
(1)µćEŌŚCAŃÓ³¤ĻßÉĻ£¬µćFŌŚBCŃÓ³¤ĻßÉĻ£¬Į¬½ÓDE£¬DF£¬
¢ŁČēĶ¼1£¬”ĻB=45”ć£¬AC=AE£¬BC=CF£¬Ēė²¹Č«Ķ¼ŠĪ£¬²¢Ö±½ÓŠ“³öDEŗĶDFµÄĪ»ÖĆ¹ŲĻµÓėŹżĮæ¹ŲĻµ£»
¢ŚČēĶ¼2£¬”ĻB=30”ć£¬ČōDEŗĶDFµÄĪ»ÖĆ¹ŲĻµĀś×ć¢ŁÖŠµÄ½įĀŪ£¬Ēė²¹Č«Ķ¼ŠĪ£¬ÅŠ¶ĻAEŗĶCFµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£»
(2)µćEŌŚÉäĻßCAÉĻ£¬µćFŌŚÉäĻßBCÉĻ£¬Į¬½ÓDE£¬DF£¬BE£¬EF£¬Čē¹ūDE”ĶDF£¬EC=8£¬EB=17£¬EF=10£¬ĒėÖ±½ÓŠ“³öACµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
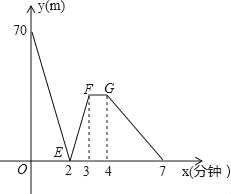
”¾ĢāÄæ”æÓŠŅ»æĘ¼¼Š”×é½ųŠŠĮĖ»śĘ÷ČĖŠŠ×ߊŌÄÜŹŌŃ飬ŌŚŹŌŃé³”µŲÓŠA”¢B”¢CČżµćĖ³“ĪŌŚĶ¬Ņ»±ŹÖ±µÄČüµĄÉĻ£¬¼×”¢ŅŅĮ½»śĘ÷ČĖ·Ö±š“ÓA”¢BĮ½µćĶ¬Ź±Ķ¬Ļņ³ö·¢£¬ĄśŹ±7·ÖÖÓĶ¬Ź±µ½“ļCµć£¬ŅŅ»śĘ÷ČĖŹ¼ÖÕŅŌ60Ć×/·ÖµÄĖŁ¶ČŠŠ×ߣ¬ČēĶ¼ŹĒ¼×”¢ŅŅĮ½»śĘ÷ČĖÖ®¼äµÄ¾ąĄėy£ØĆ×£©ÓėĖūĆĒµÄŠŠ×ߏ±¼äx£Ø·ÖÖÓ£©Ö®¼äµÄŗÆŹżĶ¼Ļó£¬Ēė½įŗĻĶ¼Ļ󣬻Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©A”¢BĮ½µćÖ®¼äµÄ¾ąĄėŹĒ”” ””Ć×£¬¼×»śĘ÷ČĖĒ°2·ÖÖÓµÄĖŁ¶ČĪŖ”” ””Ć×/·Ö£»
£Ø2£©ČōĒ°3·ÖÖÓ¼×»śĘ÷ČĖµÄĖŁ¶Č²»±ä£¬ĒóĻ߶ĪEFĖłŌŚÖ±ĻßµÄŗÆŹż½āĪöŹ½£»
£Ø3£©ČōĻ߶ĪFG”ĪxÖį£¬Ōņ“Ė¶ĪŹ±¼ä£¬¼×»śĘ÷ČĖµÄĖŁ¶ČĪŖ”” ””Ć×/·Ö£»
£Ø4£©ĒóA”¢CĮ½µćÖ®¼äµÄ¾ąĄė£»
£Ø5£©ČōĒ°3·ÖÖÓ¼×»śĘ÷ČĖµÄĖŁ¶Č²»±ä£¬Ö±½ÓŠ“³öĮ½»śĘ÷ČĖ³ö·¢¶ą³¤Ź±¼äĻą¾ą28Ć×£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚ¾ŲŠĪÖ½Ę¬ABCDÖŠ£¬![]() £¬
£¬![]() £¬·ÕŪ¾ŲŠĪÖ½Ę¬£¬Ź¹µćAĀäŌŚ¶Ō½ĒĻßDBÉĻµÄµćF“¦£¬ÕŪŗŪĪŖDE£¬“ņæŖ¾ŲŠĪÖ½Ę¬£¬²¢Į¬½ÓEF£®
£¬·ÕŪ¾ŲŠĪÖ½Ę¬£¬Ź¹µćAĀäŌŚ¶Ō½ĒĻßDBÉĻµÄµćF“¦£¬ÕŪŗŪĪŖDE£¬“ņæŖ¾ŲŠĪÖ½Ę¬£¬²¢Į¬½ÓEF£®
![]() µÄ³¤ĪŖ¶ąÉŁ£»
µÄ³¤ĪŖ¶ąÉŁ£»
![]() ĒóAEµÄ³¤£»
ĒóAEµÄ³¤£»
![]() ŌŚBEÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ
ŌŚBEÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ![]() µÄÖµ×īŠ”£æČō“ęŌŚ£¬ĒėÄć»³öµćPµÄĪ»ÖĆ£¬²¢Ēó³öÕāøö×īŠ”Öµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ×īŠ”£æČō“ęŌŚ£¬ĒėÄć»³öµćPµÄĪ»ÖĆ£¬²¢Ēó³öÕāøö×īŠ”Öµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°Ń§¶ųŹ±Ļ°Ö®£¬²»ŅąĄÖŗõ!”±£¬¹ÅČĖ°Ń¾³£ø“Ļ°µ±×÷ŹĒŅ»ÖÖĄÖȤ£¬ÄÜ“ļµ½ÕāÖÖ¾³½ēŹĒ·Ē³£²»ČŻŅ׵ģ®ø“Ļ°æÉŅŌČĆŅÅĶüµÄÖŖŹ¶µĆµ½²¹Ź°£¬ĮćÉ¢µÄÖŖŹ¶±äµĆĻµĶ³£¬±”ČõµÄÖŖŹ¶ÓŠĖłĒæ»Æ£¬ÕĘĪÕµÄÖŖŹ¶øü¼Ó¹®¹Ģ£¬ÉśŹčµÄ¼¼ÄܵƵ½ŃµĮ·£®ĪŖĮĖĮĖ½ā³õŅ»Ń§ÉśĆæÖܵÄø“Ļ°Ēéæö£¬½ĢĪń“¦¶Ō³õŅ»£Ø1£©°ąŃ§ÉśŅ»ÖÜø“Ļ°µÄŹ±¼ä½ųŠŠĮĖµ÷²é£¬ø“Ļ°Ź±¼äĖÄÉįĪåČėŗóÖ»ÓŠ4ÖÖ£ŗ1Š”Ź±£¬2Š”Ź±£¬3Š”Ź±£¬4Š”Ź±£¬Ņ»ÖÜø“Ļ°2Š”Ź±µÄÅ®ÉśČĖŹżÕ¼Č«°ąČĖŹżµÄ16%£¬Ņ»ÖÜø“Ļ°4Š”Ź±µÄÄŠÅ®ÉśČĖŹżĻąµČ£®øł¾Żµ÷²é½į¹ū£¬ÖĘ×÷ĮĖĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£Ø±ķ£©£ŗ

·Ö×é£ØĖÄÉįĪåČėŗó£© | ʵŹż£ØѧɜČĖŹż£© |
1Š”Ź± | 2 |
2Š”Ź± | a |
3Š”Ź± | 4 |
4Š”Ź± | b |
³õŅ»£Ø1£©°ąÅ®ÉśµÄø“Ļ°Ź±¼äŹż¾Ż£Øµ„Ī»£ŗŠ”Ź±£©ČēĻĀ£ŗ0.9£¬1.3£¬1.7£¬1.8£¬1.9£¬2.2£¬2.2£¬2.2£¬2.3£¬2.4£¬3.2£¬3.2£¬3.2£¬3.3£¬3.8£¬3.9£¬3.9£¬4.1£¬4.2£¬4.3£®
Å®ÉśŅ»ÖÜø“Ļ°Ź±¼äʵŹż·Ö²¼±ķ
£Ø1£©ĖÄÉįĪåČėĒ°£¬Å®ÉśŅ»ÖÜø“Ļ°Ź±¼äµÄÖŚŹżĪŖ______Š”Ź±£¬ÖŠĪ»ŹżĪŖ______Š”Ź±£»
£Ø2£©Ķ³¼ĘĶ¼±ķÖŠa=______£¬c=______£¬³õŅ»£Ø1£©°ąÄŠÉśČĖŹżĪŖ______ČĖ£¬øł¾ŻÉČŠĪĶ³¼ĘĶ¼¹ĄĖć³õŅ»£Ø1£©°ąÄŠÉśŅ»ÖܵÄĘ½¾łø“Ļ°Ź±¼äĪŖ______Š”Ź±£»
£Ø3£©ĪŖĮĖ¼¤ĄųѧɜŃų³ÉĮ¼ŗƵÄø“Ļ°Ļ°¹ß£¬½ĢĪń“¦¾ö¶Ø¶ŌŅ»ÖÜø“Ļ°Ź±¼äĖÄÉįĪåČėŗó“ļµ½3Š”Ź±¼°ŅŌÉĻµÄČ«Äź¼¶Ń§Éś½ųŠŠ±ķŃļ£¬ĆæČĖ½±Ąų1øö±Ź¼Ē±¾£¬³õŅ»Äź¼¶¹²ÓŠ1000Ćūѧɜ£¬ĒėĪŹ½ĢĪń“¦Ó¦øĆ×¼±ø“óŌ¼¶ąÉŁøö±Ź¼Ē±¾£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æø½¼ÓĢā£ŗ£Øy©z£©2+£Øx©y£©2+£Øz©x£©2=£Øy+z©2x£©2+£Øz+x©2y£©2+£Øx+y©2z£©2£®
Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻÖ“ś»„ĮŖĶų¼¼ŹõµÄ¹ć·ŗÓ¦ÓĆ£¬“ßÉśĮĖæģµŻŠŠŅµµÄøßĖŁ·¢Õ¹£®Š”Ć÷¼Ę»®øųÅóÓŃæģµŻŅ»²æ·ÖĪļĘ·£¬¾ĮĖ½āÓŠ¼×”¢ŅŅĮ½¼ŅæģµŻ¹«Ė¾±Č½ĻŗĻŹŹ£®¼×¹«Ė¾±ķŹ¾£ŗæģµŻĪļĘ·²»³¬¹ż1Ē§æĖµÄ£¬°“ĆæĒ§æĖ22ŌŖŹÕ·Ń£»³¬¹ż1Ē§æĖ£¬³¬¹żµÄ²æ·Ö°“ĆæĒ§æĖ15ŌŖŹÕ·Ń£®ŅŅ¹«Ė¾±ķŹ¾£ŗ°“ĆæĒ§æĖ16ŌŖŹÕ·Ń£¬Įķ¼Ó°ü×°·Ń3ŌŖ£®É芔Ć÷æģµŻĪļĘ·xĒ§æĖ£®
(1)Ēė·Ö±šŠ“³ö¼×”¢ŅŅĮ½¼ŅæģµŻ¹«Ė¾æģµŻøĆĪļĘ·µÄ·ŃÓĆy(ŌŖ)Óėx(Ē§æĖ)Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
(2)Š”Ć÷Ń”ŌńÄļŅæģµŻ¹«Ė¾øüŹ”Ē®£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
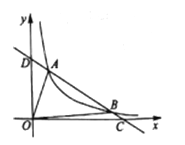
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=ax+bÓė·“±ČĄżŗÆŹż![]() (x>0)µÄĶ¼Ļń½»ÓŚµćA£Ø2£¬5£©ŗĶµćB£Øm£¬1£©.
(x>0)µÄĶ¼Ļń½»ÓŚµćA£Ø2£¬5£©ŗĶµćB£Øm£¬1£©.
£Ø1£©Č·¶ØÕāĮ½øöŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©Ēó³ö”÷OABµÄĆ껿£»
£Ø3£©½įŗĻĶ¼Ļń£¬Ö±½ÓŠ“³ö²»µČŹ½![]() µÄ½ā¼Æ.
µÄ½ā¼Æ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2019Äź“ŗ½Ś£¬Š”ÄČ¼Ņ¹ŗĀņĮĖ4øöµĘĮż£¬µĘĮżÉĻ·Ö±šŠ“ÓŠ”°»¶”±”¢”°¶Č”±”¢”°“ŗ”±”¢”°½Ś”±£ØĶā¹ŪĶźČ«Ņ»Ńł£©£®
£Ø1£©Š”ÄČ³éµ½”°2019Äź”±ŹĒ””””ŹĀ¼ž£¬”°»¶”±×Ö±»³éÖŠµÄŹĒ””””ŹĀ¼ž£»£ØĢī”°²»æÉÄÜ”±»ņ”°±ŲČ»”±»ņ”°Ė껜”±£©£®Š”ÄČ“ÓĖÄøöµĘĮżÖŠČĪČ”Ņ»øö£¬Č”µ½”°“ŗ”±µÄøÅĀŹŹĒ””””£®
£Ø2£©Š”ÄČ“ÓĖÄøöµĘĮżÖŠĻČŗóČ”³öĮ½øöµĘĮż£¬ĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼·ØĒóŠ”ÄČĒ”ŗĆČ”µ½”°“ŗ”±”¢”°½Ś”±Į½øöµĘĮżµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com