练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，PA，PB切⊙O于点A，B，点C是优弧$\widehat{AB}$上一点，若∠P=50°，则∠C=65°．

    分析 由PA与PB都为圆的切线，利用切线的性质得到两个角为直角，根据∠P的度数，利用四边形的内角和定理求出∠AOB的度数，再利用同弧所对的圆心角等于所对圆周角的2倍，求出∠ACB的度数即可．

    解答 解：如图所示，连接OA、OB．

    ∵PA、PB都为圆O的切线，
    ∴∠PAO=∠PBO=90°．
    ∵∠P=50°，
    ∴∠AOB=130°．
    ∴∠C=$\frac{1}{2}$∠AOB=$\frac{1}{2}×130°$=65°．
    故答案为：65°．

    点评 此题考查了切线的性质，圆周角定理，以及四边形的内角和，熟练掌握切线的性质是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图．在平行四边形ABCD中，AE∥CF，求证：BE=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

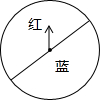    18．如图是一个红，蓝两色各占一半的转盘，小李与小明做“配紫色”的游戏．规则是：两人各让转盘自由转动一次．当转盘停止转动时．如果指针所在区域的颜色配成紫色．小明胜：如果指针所在区域的颜色配不成紫色．小李胜．在这个游戏中．小李与小明获胜的概率分别是多少？该游戏规则对双方公平吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

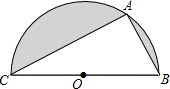    15．半圆内有一个直角三角形ABC，AB长为a厘米，AC长为b厘米，半圆的半径为r厘米，解答下面各题：
    （1）请列式表示阴影部分的面积．
    （2）若a=6，b=8，r=5，求阴影部分的面积（计算结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．设x1，x2是一元二次方程x2+4x-3=0的两个根，则2x1（x22+5x2-3）=-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，在⊙O中，AB为直径，AD为弦，过点B的切线与AD的延长线交于点C，且AD=DC，求∠ABD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

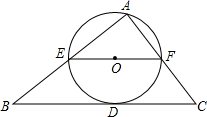    19．如图，⊙O过点A且与△ABC的边BC相切于D，与AB、AC分别交于E、F，EF经过圆心O，且EF∥BC，若EF=10，BD=12，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）计算：$\sqrt{27}$+（-2）2-（π-2015）0×|-6|-tan60°
    （2）解方程组：$\left\{\begin{array}{l}x-4y=-1\\ 2x+y=16\end{array}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．一只蚂蚁从数轴上A点出发爬了4个单位长度到了表示-1的点B，则点A所表示的数是-5或3．

    查看答案和解析>>

    同步练习册答案