
如图1,矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
|
|
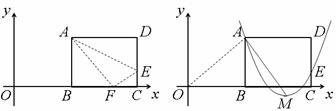
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图2,设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连结AM,
若∠OAM=90°,求a、h、m的值.
解:(1)∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°.
由折叠对称性:AF=AD=10,FE=DE.
在Rt△ABF中,BF= .
.
∴FC=4.
在Rt△ECF中,42+(8-x)2=x2,解得x=5.
∴CE=8-x=3.
∵B(m,0),∴E(m+10,3),F(m+6,0).
(2)分三种情形讨论:
若AO=AF,∵AB⊥OF,∴OB=BF=6.∴m=6.
若OF=AF,则m+6=10,解得m=4.
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴(m+6)2= m2+64,解得m=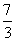 .
.
综合得m=6或4或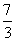 .
.
(3)由(1)知A(m,8),E(m+10,3).
依题意,得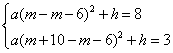 ,
,
解得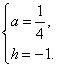
∴M(m+6,﹣1).
设对称轴交AD于G.
∴G(m+6,8),∴AG=6,GM=8-(﹣1)=9.
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG.
又∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG.
∴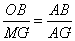 ,即
,即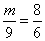 .
.
∴m=12.


科目:初中数学 来源: 题型:
2014年3月5日,第十二届全国人民代表大会第二次会议在人民大会堂开幕,国务院总理李克强作《政府工作报告》。报告指出我国2013年国内生产总值达到569000亿元。“569000”这个数据用科学记数法(保留两个有效数字)表示正确的是:……………………( )
A.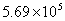 B.
B.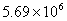 C.
C. D.
D.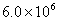
查看答案和解析>>
科目:初中数学 来源: 题型:
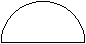
小明打算用一张半圆形的纸做一个圆锥。在制作过程中,他先将半圆剪成面积比为1:2的两个扇形.
(1)请你在图中画出他的裁剪痕迹.(要求尺规作图,不写作法,保留作图痕迹)
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高。
查看答案和解析>>
科目:初中数学 来源: 题型:
孙杨正在为备战第15届游泳世锦赛而刻苦训练. 为判断他的成绩是否稳定,教练要对他10次训练的成绩进行统计分析,则教练需了解 10次成绩的( )
A.方差 B.众数 C.平均数 D.频数
D.频数
查看答案和解析>>
科目:初中数学 来源: 题型:
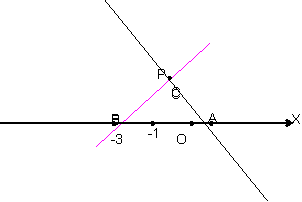
在平面直角坐标系中,点O是原点。直线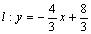 与x轴交于点A,过点B(-3,0)作BC⊥l,垂足为C,点D是直线BC上的一个动点;
与x轴交于点A,过点B(-3,0)作BC⊥l,垂足为C,点D是直线BC上的一个动点;
(1)求直线与y轴的交点P的坐标和线段BC的长度
(2)若CD=1,求点D的坐标;
‚过点D做直线m∥l,交x轴于点E,连接CE,,当点D在线段CB上运动时,求出使得三角形CDE的面积最大时点D的位置;
ƒ在直线C
|
 存在点
存在点 D使三角形CDE的面积等于
D使三角形CDE的面积等于
|
 | |||
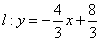 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com