
【题目】已知关于 ![]() 的方程
的方程 ![]() .
.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求整数 ![]() 的值.
的值.
【答案】
(1)
证明:∵ ![]() ,
,
∴ ![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
∵ ![]()
![]()
![]() 恒成立
恒成立
∴此方程总有两个不相等的实数根
(2)
解: ![]() ,
,
∴ ![]() .
.
∵方程的两个实数根都是整数,且m是整数,
∴ ![]() 或
或 ![]()
【解析】(1)计算出△的值,即可判定方程总有两个不相等的实数根;
(2)解方程求得 ![]() ,再由方程的两个实数根都是整数,且m是整数,即可求得m的值.
,再由方程的两个实数根都是整数,且m是整数,即可求得m的值.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】若a=255 ,b=344,c=433,则a ,b,c 大小关系是( )
A. b>c>a B. a>b>c C. c>a>b D. a<b<c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
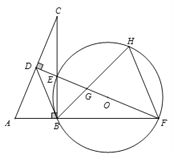
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E , 交BC的延长线于点F . 
(1)求证:BF=CD;
(2)连接BE , 若BE⊥AF , ∠F=60°, ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com