
����Ŀ��ij��ѧ�ţ�1����Ϊ���˽�ȫ��ѧ��ϲ���������������ȡȫ�����ķ�����������ƹ��������������ĸ����������ȫ��ѧ������Ȥ���ã����ݵ���Ľ���齨��4����ȤС�飬�����Ƴ���ͼ��ʾ��������������ͳ��ͼ����ͼ�٣��ڣ�Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺
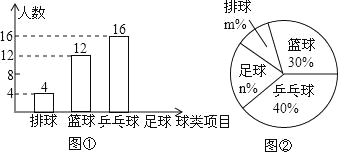
��1���ţ�1�����ѧ������Ϊ ����������ͳ��ͼ����������
��2������ͳ��ͼ��m= ��n= ����ʾ���������ε�Բ�Ľ��� �ȣ�
��3��������ȤС��4��ѧ������3��1Ů�����ڴ���������ѡ��2��ѧ���μ�ѧУ������ӣ������б�����״ͼ�ķ�����ѡ����2��ѧ��ǡ����1��1Ů�ĸ��ʣ�
���𰸡���1��40����2��10��20��72����3��![]() .
.
��������
�����������1������ϲ���������������ռ�İٷֱ���ʽ���㼴�����ѧ�����������������ϲ�������������Ȼ��ȫͳ��ͼ���ɣ�
��2���ֱ����ϲ������ϲ������İٷֱȼ��ɵõ�m��n��ֵ����ϲ�������������ռ�İٷֱȳ���360�㼴�ɣ�
��3��������״ͼ��Ȼ����ݸ��ʹ�ʽ��ʽ���㼴�ɵý⣮
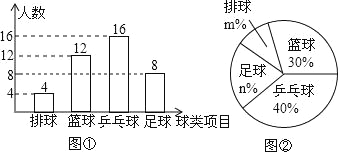
�����������1���ţ�1�����ѧ������Ϊ��12��30%=40���ˣ���
ϲ�����������Ϊ��40-4-12-16=40-32=8���ˣ���
��ȫͳ��ͼ��ͼ��ʾ��
��2����![]() ��100%=10%��
��100%=10%��
![]() ��100%=20%��
��100%=20%��
��m=10��n=20��
��ʾ���������ε�Բ�Ľ���20%��360��=72�㣻
��3���������⻭����״ͼ���£�
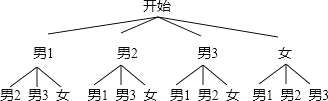
һ����12�������ǡ����1��1Ů�������6�֣�
��P��ǡ����1��1Ů��=![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�Ķ���O������ԭ�㣬��OA�ߺ�AB������ֱ�ߵĽ���ʽ�ֱ�Ϊ��![]() ��
��![]() ��
��
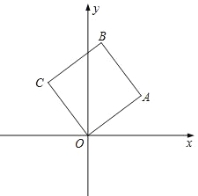
��1����������OABC�ı߳���
��2�����ж���P��Q�ֱ��C��Aͬʱ��������P���߶�CB���յ�B�˶����ٶ�Ϊÿ��1����λ����Q������A��O��C���յ�C�˶����ٶ�Ϊÿ��k����λ�����˶�ʱ��Ϊ2�룮��kΪ��ֵʱ������CPQ������һ�߷��ۣ�ʹ�÷���ǰ���������������ɵ��ı���Ϊ���Σ�
��3������������ÿ��![]() ����λ���ٶ�������AO�»���ֱ������C����x����ʱֹͣ�»�������������x���·����ֵ����ΪS����S���ڻ���ʱ��t�ĺ�����ϵʽ����д����Ӧ�Ա���t��ȡֵ��Χ��
����λ���ٶ�������AO�»���ֱ������C����x����ʱֹͣ�»�������������x���·����ֵ����ΪS����S���ڻ���ʱ��t�ĺ�����ϵʽ����д����Ӧ�Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������10����ˮ�������г���һ�ָߵ�ˮ��,���ÿǧ��ӯ����ë������10Ԫ,ÿ����۳�500ǧ�������г����鷢��,�ڽ����۲���������,��ÿǧ���Ǽ�1Ԫ,������������20ǧ����
��1������ÿǧ����ӯ��18Ԫ�ĵ��۳���,��ÿ�����ë����Ϊ����Ԫ?
��2�����г�Ҫ��֤ÿ����ë����6000Ԫ,ͬʱ��Ҫʹ�˿͵õ�ʵ��,��ÿǧ��Ӧ�Ǽ۶���Ԫ?
��3�����谴ë�����10%���ɸ���˰��,�˹���ÿ�հ�������ÿǧ��֧��0��9Ԫ,ˮ�緿���ÿ��102Ԫ,��ʣ�µ�ÿ���ܴ�����Ҫ�ﵽ5100Ԫ,��ÿǧ���Ǽ�ӦΪ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ�ļ���ѧУ�ľ����Ϊ3000�ף���ͬѧ�Ȳ���600�ף�Ȼ��˹�����ȥѧУ����ͬѧ�����г�ȥѧУ����֪�ײ����ٶ����������г��ٶȵ�![]() �����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
�����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
��1�����������г����ٶȣ�
��2��������ѧУʱ����ͬѧ��ѧУ���ж�Զ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com