
 一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.
一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题. =30(cm);
=30(cm);
 (cm),
(cm), +25=
+25= +25.
+25. +25)cm.
+25)cm.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.
一天,数学学习小组的三名同学小聪、小明、小雨发现一把30°的直角尺斜靠在教室的墙角(如图,△ABC中的直角边BC长为50cm),小聪提议针对这一现象,每人提出一个数学问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 一天,数学老师布置一个思考题,要求每个学习小组课后去讨论.你能和他们一起思考吗?题目是这样的:
一天,数学老师布置一个思考题,要求每个学习小组课后去讨论.你能和他们一起思考吗?题目是这样的:查看答案和解析>>
科目:初中数学 来源: 题型:
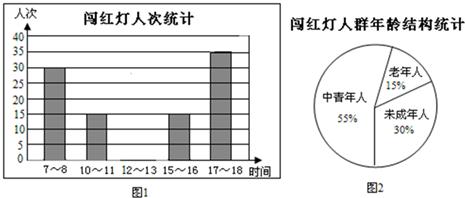
某校数学学习小组利用双休日对家乡县城区人们的交通意识进行调研.在城区中心交通最拥挤的一个十字路口,观察、统计白天抽取几个时段中闯红灯的人次.制作了如下的两个数据统计图.

1.若老年人这一天闯红灯人次为18人,求图1提供的五个数据(各时段闯红灯人次)的中位数并补全条形图;
2.估计一个月(按30天计算)白天在该十字路口闯红灯的未成年人约有多少人次?
3.请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com