
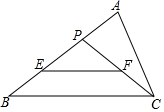
 如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )
如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )| A. | S1=$\frac{1}{3}$S | B. | S1=$\frac{1}{4}$S | C. | S1=$\frac{2}{3}$S | D. | S1=$\frac{1}{6}$S |
分析 先利用三角形中位线的性质得到EF∥BC,EF=$\frac{1}{2}$BC,则可判断△PEF∽△PBC,利用相似三角形的性质得$\frac{{S}_{1}}{{S}_{△PBC}}$=$\frac{1}{4}$,接着利用三角形面积公式得到S△PBC:S△PAC=1:2,所以S△PBC=2S1,于是得到S=6S1.
解答 解:∵E、F分别是PB,PC的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,
∴$\frac{{S}_{1}}{{S}_{△PBC}}$=($\frac{EF}{BC}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,
即S△PBC=4S1,
∵AP:BP=1:2,
∴S△PBC:S△PAC=1:2,
∴S△PBC=2S1,
∴S=4S1+2S1=6S1,
即S1=$\frac{1}{6}$S.
故选D.
点评 三本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时,主要利用相似比计算线段的长或利用相似比表示面积之间的关系.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
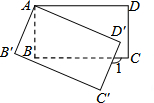 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,若旋转角为20°,则∠1为( )| A. | 110° | B. | 120° | C. | 150° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-1 | B. | a=0 | C. | a=$\frac{1}{2}$ | D. | a=$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,对称轴是x=-1,下列结论:(1)ac<0;(2)4ac<b2;(3)2a+b=0;(4)a-b+c>2,其中正确的结论共有( )
二次函数y=ax2+bx+c的图象如图所示,对称轴是x=-1,下列结论:(1)ac<0;(2)4ac<b2;(3)2a+b=0;(4)a-b+c>2,其中正确的结论共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com