
 一块庄稼地是长40m,宽30m的长方形,受灾面积正好是与对角线垂直方向的一条带状区(如图所示,平行四边形AECF为受灾面积),那么对这块庄稼地来说,受灾面积多大?
一块庄稼地是长40m,宽30m的长方形,受灾面积正好是与对角线垂直方向的一条带状区(如图所示,平行四边形AECF为受灾面积),那么对这块庄稼地来说,受灾面积多大? 分析 先利用勾股定理求出BD,再根据$\frac{1}{2}$AD•AB=$\frac{1}{2}$BD•AH,求出AH,由cos∠DAH=$\frac{AH}{AD}$=$\frac{AD}{AF}$,求出AF,根据勾股定理求出DF,即可解决问题.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD=BC=30,AB=CD=40,∠DAB=90°,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{3{0}^{2}+4{0}^{2}}$=50,
∵AH⊥BD,
∴$\frac{1}{2}$AD•AB=$\frac{1}{2}$BD•AH,
∴AH=24,
∵cos∠DAH=$\frac{AH}{AD}$=$\frac{AD}{AF}$,
∴AF=37.5,
∴DF=$\sqrt{A{F}^{2}-A{D}^{2}}$=22.5,
∴CF=CD-DF=17.5,
∴这块庄稼地来说,受灾面积=CF•AD=17.5×30=525m2.
点评 本题考查矩形的性质平行四边形的性质、勾股定理等知识,学会直角三角形斜边上的高的求法是解题的关键,属于中考常考题型.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
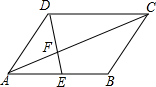 如图,?ABCD中,AE:EB=2:3,DE交AC于F.
如图,?ABCD中,AE:EB=2:3,DE交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,点A(6,0),点B(0,8),点C在y轴上,将△OAB沿AC对折,使点O落在AB边上的点D处.
已知如图,点A(6,0),点B(0,8),点C在y轴上,将△OAB沿AC对折,使点O落在AB边上的点D处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com