
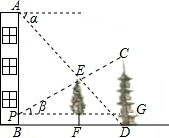
 如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)
如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号) 分析 根据题意求出∠BAD=∠ADB=45°,进而根据等腰直角三角形的性质求得FD,在Rt△PEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△PCG中,继而可求出CG的长度.
解答  解:由题意可知∠BAD=∠ADB=45°,
解:由题意可知∠BAD=∠ADB=45°,
∴FD=EF=6米,
在Rt△PEH中,∵tanβ=$\frac{EH}{PH}$=$\frac{5}{BF}$,
∴BF=$\frac{5}{\frac{\sqrt{3}}{3}}$=5$\sqrt{3}$,
∴PG=BD=BF+FD=5$\sqrt{3}$+6,
在RT△PCG中,∵tanβ=$\frac{CG}{PG}$,
∴CG=(5$\sqrt{3}$+6)•$\frac{\sqrt{3}}{3}$=5+2$\sqrt{3}$,
∴CD=(6+2$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
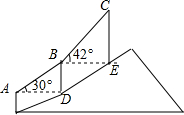 如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.85×105 | B. | 1.85×104 | C. | 1.8×105 | D. | 18.5×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
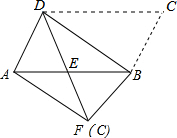 如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com