
【题目】已知抛物线C1:y=﹣x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B.若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
A.![]()
B.![]()
C.![]()
D.![]()
 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式;
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE= ![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
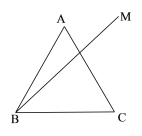
【题目】如图,等边△ABC中,BM是ABC内部的一条射线,且![]() ,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
,点A关于BM的对称点为D,连接AD,BD,CD,其中AD、CD的延长线分别交射线BM于点E,P.
(1)依题意补全图形;
(2)若ABM ,求BDC 的大小(用含的式子表示);
(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() ,其中
,其中![]() ,
,![]() ,
,![]() )的直角顶点
)的直角顶点![]() 重叠在一起.
重叠在一起.

(1)如图1,当![]() 平分
平分![]() 时,
时,![]() 是多少度?
是多少度?
(2)如图2,当![]() 不平分
不平分![]() 时,
时,![]() 是多少度?
是多少度?
(3)当![]() 的余角的4倍等于
的余角的4倍等于![]() 时,求此时
时,求此时![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需要将方向调整到与出发时一致,则方向的调整应为( )
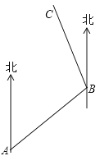
A.左转80°B.右转80°C.左转100°D.右转100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
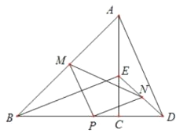
【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。因为EF∥AD,所以 ∠2 = 。又因为 ∠1 = ∠2,所以 ∠1 = ∠3。 所以AB∥ 。所以∠BAC + = 180°。又因为∠BAC = 70°,所以∠AGD = 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com