
 的度数为280°,D是由弦AB与优弧
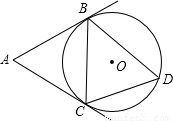
的度数为280°,D是由弦AB与优弧 所围成的弓形区域内的任意点,连接AD、BD.试判断∠ADB的度数范围?并说明理由.
所围成的弓形区域内的任意点,连接AD、BD.试判断∠ADB的度数范围?并说明理由.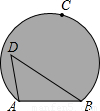
 的度数,求出
的度数,求出 所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围.
所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围. 于E点,连接EB,(2分)
于E点,连接EB,(2分)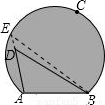
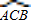 =280°,
=280°, (360°-
(360°-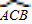 )=40°,(2分)
)=40°,(2分)

科目:初中数学 来源:第3章《圆》常考题集(19):3.5 直线和圆的位置关系(解析版) 题型:填空题
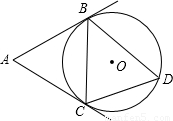
查看答案和解析>>
科目:初中数学 来源:第24章《圆(下)》常考题集(04):24.2 圆的切线(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2007-2008学年江苏省苏州市吴江市九年级(上)期末数学试卷(解析版) 题型:填空题
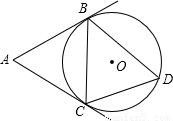
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(07)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com