
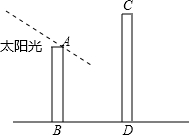
 如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.
如图,AB为某一小区内的居民楼,高为18米,为缓解住房紧张的状况,现决定在这栋居民楼后面盖一栋新楼(图中CD),它的一楼是6米高的小区超市,当太阳光与水平线的夹角为30°时.分析 (1)利用三角函数算出阳光可能照到居民楼的什么高度,和6米进行比较.
(2)超市不受影响,说明30°的阳光应照射到楼的底部,根据新楼的高度和30°的正切值即可计算.
解答 解:(1)如图1所示:
过F点作FE⊥AB于点E,
∵EF=15米,∠AFE=30°,
∴AE=5$\sqrt{3}$米,
∴EB=FC=(18-5$\sqrt{3}$)米,
∵18-5$\sqrt{3}$>6
∴超市以上的居民住房采光要受影响;
(2)如图2所示:若要使超市采光不受影响,则太阳光从A直射到C处.
∵AB=18米,∠ACB=30°
∴BC=$\frac{AB}{tan30°}$=$\frac{18}{\frac{\sqrt{3}}{3}}$=18$\sqrt{3}$≈32米,
答:若要使超市采光不受影响,两楼最少应相距32米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.


科目:初中数学 来源: 题型:解答题
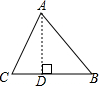 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
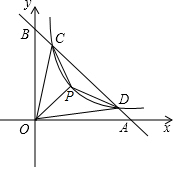 如图,已知C,D是反比例函数y=$\frac{m}{x}$图象在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x1,y1),(x2,y2),连结OC,OD.
如图,已知C,D是反比例函数y=$\frac{m}{x}$图象在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x1,y1),(x2,y2),连结OC,OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
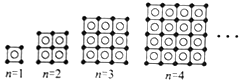 下列各个图形中,“•”的个数用a表示,“○”的个数用b表示,如:n=1时,a=4,b=1;n=2时,a=9,b=4;…根据图形的变化规律,当n=2017时,$\sqrt{a}$+$\sqrt{b}$的值为4035.
下列各个图形中,“•”的个数用a表示,“○”的个数用b表示,如:n=1时,a=4,b=1;n=2时,a=9,b=4;…根据图形的变化规律,当n=2017时,$\sqrt{a}$+$\sqrt{b}$的值为4035.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com