
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
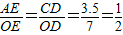 ,结合OA=
,结合OA=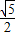 ,可求A点坐标,从而求出B点坐标.由抛物线过O、B、C三点求出解析式;
,可求A点坐标,从而求出B点坐标.由抛物线过O、B、C三点求出解析式;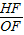 ,即顶点H的纵坐标与横坐标之比,求顶点坐标求解.
,即顶点H的纵坐标与横坐标之比,求顶点坐标求解.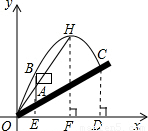 解:(1)作CD⊥OX于D点,HF⊥OX于F,延长BA交OX于E点.
解:(1)作CD⊥OX于D点,HF⊥OX于F,延长BA交OX于E点.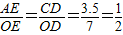 ,即OE=2AE,
,即OE=2AE,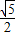 ,根据勾股定理可得AE=
,根据勾股定理可得AE= ,OE=1,
,OE=1,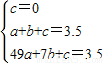
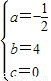
 x2+4x
x2+4x x2+4x=-
x2+4x=- (x2-8x)=-
(x2-8x)=- (x-4)2+8,
(x-4)2+8,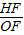 =
= =2.
=2.

科目:初中数学 来源:2001年青海省中考数学试卷(解析版) 题型:解答题
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《锐角三角函数》(02)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《三角形》(03)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2001年青海省中考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com