练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．一个三角形木板，去了一个角，你能作出所缺角的平分线所在的直线吗？能．（填“能”或“不能”）

    分析 先作出其它两角的角平分线交于点E，再延长两边交于一点F，连接EF，直线EF就是所缺角的平分线所在的直线．

    解答 解：如图：先作出其它两角的角平分线交于点E，再延长两边交于一点F，连接EF，直线EF就是所缺角的平分线所在的直线．

    故答案为：能．

    点评 本题主要考查了作图及应用，解题的关键是熟记三角形的三条角平分线交于一点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．可证：AE⊥BF；
    （1）将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM，如图2，若AM和BF相交于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．
    （2）将△BCF沿BF对折，得到△BPF，如图3，延长FP交BA的延长线于点Q，求sin∠BQP的值；

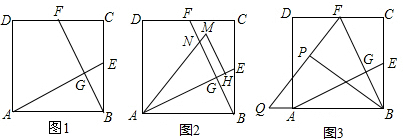
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知方程x2+nx-1=0的两实数根分别为α、β，则$\frac{β}{α}$+$\frac{α}{β}$的值为（　　）
    A．n2+2B．-n2+2C．n2-2D．-n2-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．某洗衣机洗涤衣服时，经历了进水，清洗，排水脱水四个连续的过程，其中进水，清洗，排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如图折线图所示，已知清洗时间为11分钟，排水时间为2分钟，则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列方程中：①x+y=x2；②$\frac{{x}^{3}}{x}$-x=0；③（x2-1）（x+1）=x（5+x）；④$\sqrt{5}$t2-6t=0；⑤y2=6；⑥$\frac{x}{3}$-1=$\frac{{x}^{2}}{4}$，属于一元二次方程的是（　　）
    A．①④⑤B．③④⑤C．④⑤⑥D．②⑤⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．已知关于x的方程$\frac{1}{4}$x2-（m-2）x+m2=0有两个相等的实数根，则方程的根为（　　）
    A．x1=x2=1B．x1=x2=-2C．x1=x2=-1D．x1=x2=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．小明用17元买了1支笔和某种笔记本3个，已知笔记本的单价比笔的单价的2倍还多1元，设笔每支x元，笔记本每本y元，则所列方程组为（　　）
    A．$\left\{\begin{array}{l}{x+3y=17}\\{x=2y+1}\end{array}\right.$B．$\left\{\begin{array}{l}{x+3y=17}\\{y=2x+1}\end{array}\right.$C．$\left\{\begin{array}{l}{y+3x=17}\\{x=2y+1}\end{array}\right.$D．$\left\{\begin{array}{l}{y+3x=17}\\{y=2x+1}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如果方程x2+px+q=0的两个根是x1、x2，那么x1+x2=-p，x1•x2=q，请根据以上结论，解决下列问题：
    （1）已知x1、x2是方程x2+4x-2=0的两个实数根，求$\frac{1}{x_1}$+$\frac{1}{x_2}$的值；
    （2）已知方程x2+bx+c=0的两根分别为$\sqrt{2}$+1、$\sqrt{2}$-1，求出b、c的值；
    （3）关于x的方程x2+（m-1）x+m2-3=0的两个实数根互为倒数，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案