
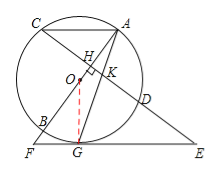
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
【答案】(1)相切,理由见解析;(2)4.
【解析】
试题分析:(1)求出∠OGA=∠OAG,∠AKH+∠OAG=90°,∠KGE=∠GKE=∠AKH,推出∠KGE+∠OGA=∠AKH+∠OAG=90°,得出∠OGE=90°,根据切线的判定推出即可;
(2)求出∠F=∠CAH,∠OGF=∠CHA=90°,推出Rt△AHC∽Rt△FGO,得出![]() ,根据
,根据![]()
求出![]() ,得出方程
,得出方程![]() ,解出即可.
,解出即可.
试题解析:(1)如图,连接OG.
∵OA=OG,∴∠OGA=∠OAG.
∵CD⊥AB,∴∠AKH+∠OAG=90°.
∵KE=GE,
∴∠KGE=∠GKE=∠AKH.
∴∠KGE+∠OGA=∠AKH+∠OAG=90°.
∴∠OGE=90°,即OG⊥EF.
又∵G在圆O上,∴EF与圆O相切.
(2)∵AC∥EF, ∴∠F=∠CAH,
∴Rt△AHC∽ Rt△FGO. ∴![]() .
.
∵在Rt△OAH中,![]() ,设AH=3t,则AC=5t,CH=4t.
,设AH=3t,则AC=5t,CH=4t.
∴![]() . ∴
. ∴![]() .
.
∵FB=1 ∴![]() ,解得:OG=4.
,解得:OG=4.
∴圆O的半径为4 .


科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字1,2,3,4,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字2,4,6.小明先从A布袋中随机取出﹣个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,请画出树形图或列表写出(m,n)的所有取值;
(2)求关于x的一元二次方程x2﹣mx+![]() n=0有实数根的概率.
n=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
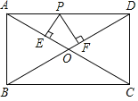
【题目】已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习概念:
三角形一边的延长线与三角形另一边的夹角叫做三角形的外角.如图1中∠ACD是△AOC的外角,那么∠ACD与∠A、∠O之间有什么关系呢?
∵∠ACD=180°﹣∠ACO,∠A+∠O=180°﹣∠ACO
∴∠ACD=∠A+ ,
结论:三角形的外角等于与它不相邻的两个内角的 .
问题探究:
(1)如图2,已知:∠AOB=∠ACP=∠BDP=60°,且AO=BO,则△AOC △OBD;
(2)如图3,已知∠ACP=∠BDP=45°,且AO=BO,当∠AOB= °,△AOC≌△OBD;
应用结论:

(3)如图4,∠AOB=90°,OA=OB,AC⊥OP,BD⊥OP,请说明:AC=CD+BD.
拓展应用:
(4)如图5,四边形ABCD,AB=BC,BD平分∠ADC,AE∥CD,∠ABC+∠AEB=180°,EB=5,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系![]() 的原点O在格点上,
的原点O在格点上, ![]() 轴、
轴、![]() 轴都在网格线上.线段AB的端点A、B在格点上.
轴都在网格线上.线段AB的端点A、B在格点上.

(1)将线段AB绕点O逆时针90°得到线段A1B1,请在图中画出线段A1B1;
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2;
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形是平行四边形时,请直接写出点P的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形。

(1)你认为图2中大正方形的边长为___;小正方形(阴影部分)的边长为___.(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(ab)![]() ,(a+b)
,(a+b)![]() ,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证。
,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生课余生活,某区教育部门准备在七年级开设兴趣课堂.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
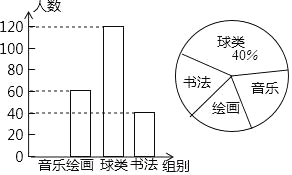
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com