
分析 (1)利用代入消元法解方程组;
(2)分别将①和②进行变形,将y的系数化为相等的-15,相减可得x的值,代入可得y的值;
(3)先去括号,整理,发现x和y的系数相反和相同,相加和相减可分别得y和x的值.
解答 解:(1)$\left\{\begin{array}{l}{x=3y+5①}\\{3y=8-2x②}\end{array}\right.$,
把①代入②得:3y=8-2(3y+5),
3y=8-6y-10,
9y=-2,
y=-$\frac{2}{9}$③,
把③代入①得:x=3×$(-\frac{2}{9})$+5=$\frac{13}{3}$,
∴方程组的解为:$\left\{\begin{array}{l}{x=\frac{13}{3}}\\{y=-\frac{2}{9}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x-3y=8①}\\{7x-5y=-5②}\end{array}\right.$,
①×5得:10x-15y=40③,
②×3得:21x-15y=-15④,
④-③得:11x=-55,
x=-5,
把x=-5代入①得:y=-6,
∴方程组的解为:$\left\{\begin{array}{l}{x=-5}\\{y=-6}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{5(x+y)-3(x-y)=16}\\{3(x+y)-5(x-y)=0}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{2x+8y=16①}\\{-2x+8y=0②}\end{array}\right.$,
①+②得:16y=16,
y=1,
①-②得:4x=16,
x=4,
∴方程组的解为:$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.
点评 本题考查了二元一次方程组的解法,利用消元进行求解.题目比较简单,但需要认真细心.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
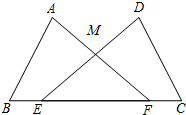 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )| A. | ∠ABF | B. | ∠BAF | C. | ∠EMF | D. | ∠AFB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
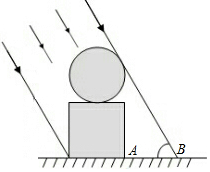 如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)
如图,广场上一个立体雕塑由两部分组成,底座是一个正方体,正上方是一个球体,且正方体的高度和球的高度相等.当阳光与地面的夹角成60°时,整个雕塑在地面上的影子AB长2米,求这个雕塑的高度.(结果精确到百分位,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com